题目
1.设随机变量X服从参数为λ的泊松分布,且 X=1 =P X=2 , 求λ.
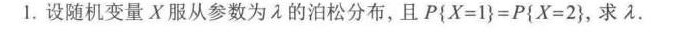
题目解答
答案
\\lambda=2.
解析
考查要点:本题主要考查泊松分布的概率公式及其应用,以及根据概率相等建立方程求解参数的能力。
解题核心思路:
- 泊松分布公式:回忆泊松分布的概率质量函数形式,即$P(X=k) = \frac{\lambda^k e^{-\lambda}}{k!}$。
- 建立方程:根据题目条件$P(X=1) = P(X=2)$,将$k=1$和$k=2$代入公式,得到关于$\lambda$的方程。
- 解方程:通过代数变形求解$\lambda$,注意排除不符合实际意义的解(如$\lambda \leq 0$)。
破题关键点:
- 正确写出泊松分布的表达式,并代入$k=1$和$k=2$的情况。
- 消去公共因子$e^{-\lambda}$简化方程。
- 验证解的合理性,确保$\lambda$为正数。
步骤1:写出泊松分布的概率公式
泊松分布的概率质量函数为:
$P(X=k) = \frac{\lambda^k e^{-\lambda}}{k!} \quad (k=0,1,2,\dots)$
步骤2:代入条件$P(X=1) = P(X=2)$
当$k=1$时:
$P(X=1) = \frac{\lambda^1 e^{-\lambda}}{1!} = \lambda e^{-\lambda}$
当$k=2$时:
$P(X=2) = \frac{\lambda^2 e^{-\lambda}}{2!} = \frac{\lambda^2 e^{-\lambda}}{2}$
根据题意,两者相等:
$\lambda e^{-\lambda} = \frac{\lambda^2 e^{-\lambda}}{2}$
步骤3:消去公共因子并解方程
两边同时除以$e^{-\lambda}$(因$e^{-\lambda} \neq 0$):
$\lambda = \frac{\lambda^2}{2}$
整理方程:
$\lambda^2 - 2\lambda = 0$
因式分解:
$\lambda(\lambda - 2) = 0$
解得:
$\lambda = 0 \quad \text{或} \quad \lambda = 2$
步骤4:验证解的合理性
泊松分布的参数$\lambda$表示平均发生次数,必须为正数,因此舍去$\lambda = 0$,最终得:
$\lambda = 2$