题目
求曲线 ^3-xy+(y)^3=1(x≥0,y≥0)上的点到坐标原点的最长距离与最短距离,
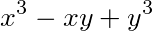 =1(x≥0,y≥0)上的点到坐标原点的最长距离与最短距离,
=1(x≥0,y≥0)上的点到坐标原点的最长距离与最短距离,
题目解答
答案
曲线上任取一点p(x,y),其到原点的距离d=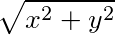 ,构造拉格朗日函数L=
,构造拉格朗日函数L=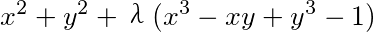 ,令
,令
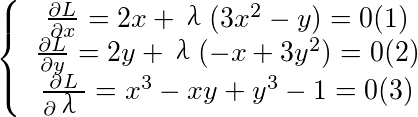
(1)-(2)得(x-y)[2+λ+3λ(x+y)]=0,即x=y或x+y=-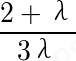 ,
,
(1)+(2)得(2-λ)(x+y)+3λ(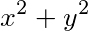 )=0.
)=0.
若x=y,代入(3)可得x=y=1,此时d=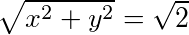 ;
;
若x+y=-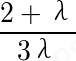 ,代入(2-λ)(x+y)+3λ(
,代入(2-λ)(x+y)+3λ(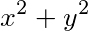 )=0可得
)=0可得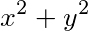 =-
=-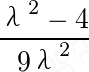 ,
,
进一步有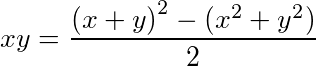 =
=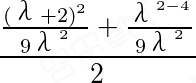 =
=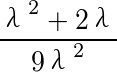 .
.
而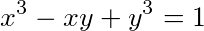 可变为(x+y)(
可变为(x+y)(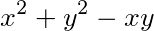 )-xy=1,把
)-xy=1,把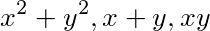 代入此方程得
代入此方程得
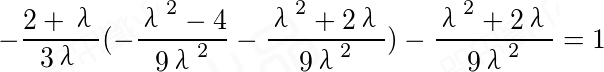 ,简化为
,简化为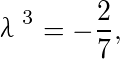 即
即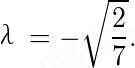
但此时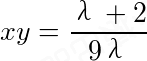 <0,不满足x≥0,y≥0,所以在x≥0,y≥0内只有一个驻点(1,1).再考虑边界上的情况,当x=0时,y=1.有
<0,不满足x≥0,y≥0,所以在x≥0,y≥0内只有一个驻点(1,1).再考虑边界上的情况,当x=0时,y=1.有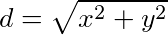 =1,
=1,
当y=0时,x=1,有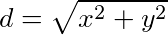 =1.
=1.
综上所述,可知最远距离为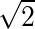 ,最近距离为1.
,最近距离为1.
解析
考查要点:本题主要考查约束条件下多元函数的极值求解,涉及拉格朗日乘数法的应用,以及边界条件分析的能力。
解题核心思路:
- 构造拉格朗日函数,将距离平方作为目标函数,约束条件为给定曲线方程。
- 联立方程求驻点,通过消元或对称性假设(如$x=y$)简化计算。
- 验证解的合理性,排除不满足$x \geq 0, y \geq 0$的解。
- 分析边界情况,即$x=0$或$y=0$时的取值,综合比较所有可能情况。
破题关键点:
- 对称性假设:通过$x=y$快速找到有效驻点$(1,1)$。
- 边界条件处理:当$x=0$或$y=0$时,直接代入约束方程求解。
- 排除无效解:非对称解可能导致$xy<0$,需舍弃。
构造拉格朗日函数
目标函数为距离平方$d^2 = x^2 + y^2$,约束条件为$x^3 - xy + y^3 = 1$,构造:
$L = x^2 + y^2 + \lambda(x^3 - xy + y^3 - 1)$
求偏导并联立方程
对$x, y, \lambda$求偏导,得方程组:
$\begin{cases}2x + \lambda(3x^2 - y) = 0 \quad (1) \\2y + \lambda(-x + 3y^2) = 0 \quad (2) \\x^3 - xy + y^3 = 1 \quad (3)\end{cases}$
对称性分析
- 假设$x = y$:
代入方程$(3)$得$2x^3 - x^2 = 1$,解得$x = y = 1$,对应距离$d = \sqrt{2}$。 - 非对称情况:
通过$(1)-(2)$得$(x - y)[2 + \lambda + 3\lambda(x + y)] = 0$,若$x \neq y$,则需满足$x + y = -\frac{2 + \lambda}{3\lambda}$。进一步代入方程$(1)+(2)$并化简,最终解得$\lambda = -\sqrt{\frac{2}{7}}$,但此时$xy < 0$,与$x \geq 0, y \geq 0$矛盾,故舍弃。
边界情况分析
- 当$x = 0$时,方程$(3)$变为$y^3 = 1$,解得$y = 1$,对应$d = 1$。
- 当$y = 0$时,同理得$x = 1$,对应$d = 1$。
综合比较
唯一有效驻点$(1,1)$对应$d = \sqrt{2}$,边界点对应$d = 1$,故最远距离为$\sqrt{2}$,最近距离为$1$。