题目
进行重复独立试验,设每次试验成功的概率为p,失败的概率为-|||-=1-p(0lt plt 1).-|||-(1)将试验进行到出现一次成功为止,以X表-|||-示所需的试验次数,求X的分布律.(此时称X服-|||-从以p为参数的几何分布.)-|||-(2)将试验进行到出现r次成功为止,以Y表示所需的试验次数,求Y的分-|||-布律.(此时称Y服从以r,p为参数的巴斯卡分布或负二项分布.)-|||-(3)一篮球运动员的投篮命中率为45%.以X表示他首次投中时累计已投-|||-篮的次数,写出X的分布律,并计算X取偶数的概率.

题目解答
答案
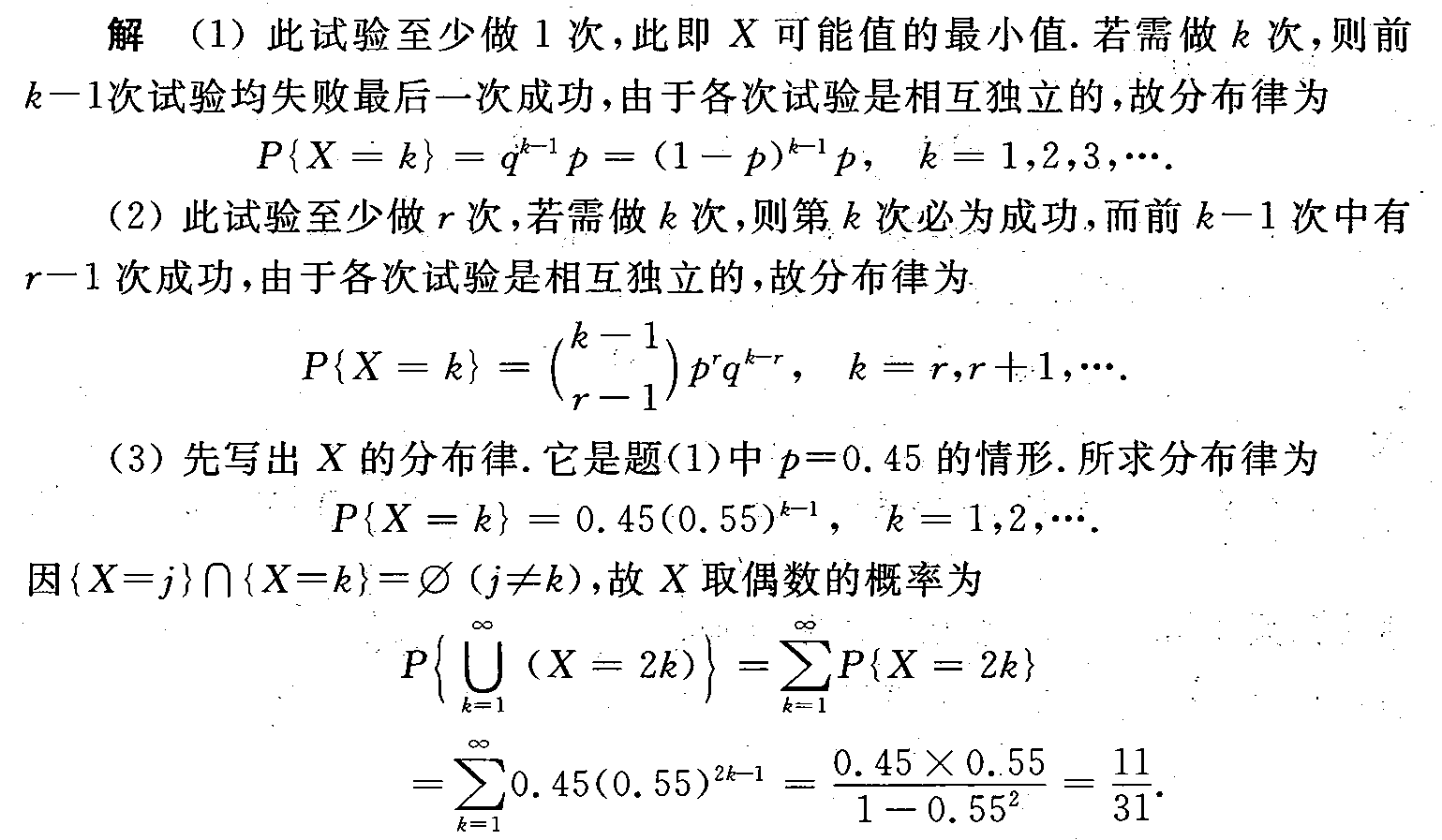
解析
- 几何分布(第1题):核心是理解“首次成功所需试验次数”的分布特点。关键点在于前$k-1$次失败,第$k$次成功,概率为$q^{k-1}p$。
- 负二项分布(第2题):需明确“第$r$次成功出现在第$k$次试验”的条件。需结合二项式系数$C(k-1, r-1)$,表示前$k-1$次中选$r-1$次成功。
- 偶数概率计算(第3题):利用几何分布的级数性质,将偶数项求和转化为等比数列求和,注意公比为$q^2$。
第(1)题
分析试验次数特点
- $X$的最小取值为$1$(首次试验成功)。
- 若需$k$次试验,则前$k-1$次均失败,第$k$次成功。
计算概率
- 由独立性,概率为$q^{k-1}p$,即:
$P\{X=k\} = (1-p)^{k-1}p, \quad k=1,2,3,\dots$
第(2)题
分析试验次数特点
- $Y$的最小取值为$r$(前$r$次均成功)。
- 若需$k$次试验,则第$k$次必成功,前$k-1$次中有$r-1$次成功。
计算概率
- 组合数$C(k-1, r-1)$表示前$k-1$次中选择$r-1$次成功的位置。
- 概率为:
$P\{Y=k\} = C(k-1, r-1) p^r (1-p)^{k-r}, \quad k=r, r+1, \dots$
第(3)题
分布律
- 直接应用第(1)题的几何分布,$p=0.45$,得:
$P\{X=k\} = 0.45 \cdot (0.55)^{k-1}, \quad k=1,2,\dots$
偶数概率计算
- 构造偶数项求和:
$P\{X \text{为偶数}\} = \sum_{k=1}^{\infty} P\{X=2k\} = \sum_{k=1}^{\infty} 0.45 \cdot (0.55)^{2k-1}$ - 提取公比:
$= 0.45 \cdot 0.55 \sum_{k=1}^{\infty} (0.55)^{2(k-1)} = 0.45 \cdot 0.55 \sum_{k=0}^{\infty} (0.55^2)^k$ - 等比数列求和:
$= \frac{0.45 \cdot 0.55}{1 - 0.55^2} = \frac{0.2475}{0.6975} = \frac{11}{31}$