题目
平面https:/img.zuoyebang.cc/zyb_443e7b4f4bf9228e9f1fec85132a95c9.jpg:2x+3y+4z+1=0 与平面https:/img.zuoyebang.cc/zyb_690f799d46d16e0cd2aba1edb9fb0e6d.jpg:2x+3y+4z+1=0的位置关系是 ( ) (A)重合(B)相交且垂直(C)平行 (D)相交且不垂直不重合
平面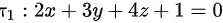 与平面
与平面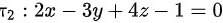 的位置关系是 ( )
的位置关系是 ( )
(A)重合
(B)相交且垂直
(C)平行
(D)相交且不垂直不重合
题目解答
答案
平面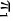 的法向量
的法向量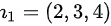
平面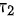 的法向量
的法向量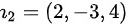
∵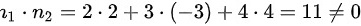
且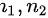 不是对应成比例,故
不是对应成比例,故
两平面既不垂直也不平行,更不重合,所以两平面相交’
故A,B,C错误D对
故答案为D
解析
步骤 1:确定平面的法向量
平面$1:2x+3y+4z+1=0$的法向量为${n}_{1}=(2,3,4)$
平面$2:2x-3y+4z-1=0$的法向量为${n}_{2}=(2,-3,4)$
步骤 2:计算法向量的点积
${n}_{1}\cdot {n}_{2}=2\cdot 2+3\cdot (-3)+4\cdot 4=4-9+16=11\neq 0$
步骤 3:判断法向量是否成比例
由于${n}_{1}$和${n}_{2}$的分量不成比例,即$\frac{2}{2}\neq \frac{3}{-3}\neq \frac{4}{4}$,所以两个平面既不平行也不重合。
步骤 4:判断平面是否垂直
由于${n}_{1}\cdot {n}_{2}\neq 0$,所以两个平面不垂直。
平面$1:2x+3y+4z+1=0$的法向量为${n}_{1}=(2,3,4)$
平面$2:2x-3y+4z-1=0$的法向量为${n}_{2}=(2,-3,4)$
步骤 2:计算法向量的点积
${n}_{1}\cdot {n}_{2}=2\cdot 2+3\cdot (-3)+4\cdot 4=4-9+16=11\neq 0$
步骤 3:判断法向量是否成比例
由于${n}_{1}$和${n}_{2}$的分量不成比例,即$\frac{2}{2}\neq \frac{3}{-3}\neq \frac{4}{4}$,所以两个平面既不平行也不重合。
步骤 4:判断平面是否垂直
由于${n}_{1}\cdot {n}_{2}\neq 0$,所以两个平面不垂直。