34.甲、乙、丙3人独立地向同一飞机射击,设击中的概率分别是0.4,0.5,0.7,若只有一人击中,则-|||-飞机被击落的概率为0.2;若有两人击中,则飞机被击落的概率为0.6;若3人都击中,则飞机一定被击-|||-落,求飞机被击落的概率.-|||-__

题目解答
答案
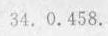
解析
本题主要考察全概率公式的应用,需先计算不同人数击中飞机的概率,再结合对应情况下飞机被击落的概率求解。
步骤1:定义事件
- 设$A$:飞机被击落;
- $B_1$:只有1人击中飞机;
- $B_2$:有2人击中飞机;
- $B_3$:3人都击中飞机;
- $B_0$:无人击中飞机(备用)。
显然$B_0,B_1,B_2,B_3$是样本空间的划分,根据全概率公式:
$P(A)=\sum_{i=0}^3 P(B_i)P(A|B_i)$
其中$P(A|B_0)=0$(无人击中则飞机不坠落),需计算$P(B_1),P(B_2),P(B_3)$及$P(A|B_1),P(A|B_2),P(A|B_3)$。
步骤2:计算各击中人数的概率
甲、乙、丙击中概率分别为$p=0.4,q=0.5,r=0.7$,独立射击:
-
$P(B_1)$:仅1人击中,分三种情况:
$\begin{align*} P(B_1)&=p(1-q)(1-r)+(1-p)q(1-r)+(1-p)(1-q)r\\ &=0.4\times0.5\times0.3 + 0.6\times0.5\times0.3 + 0.6\times0.5\times0.7\\ &=0.06 + 0.09 + 0.21\\ &=0.36 \end{align*}$ -
$P(B_2)$:仅2人击中,分三种情况:
$\begin{align*} P(B_2)&=pq(1-r)+p(1-q)r+(1-p)qr\\ &=0.4\times0.5\times0.3 + 0.4\times0.5\times0.7 + 0.6\times0.5\times0.7\\ &=0.06 + 0.14 + 0.21\\ &=0.41 \end{align*}$ -
$P(B_3)$:3人都击中:
$P(B_3)=pqr=0.4\times0.5\times0.7=0.14$
步骤3:代入全概率公式
已知:
$P(A|B_1)=0.2$,$P(A|B_2)=0.6$,$P(A|B_3)=1$,$P(A|B_0)=0$
$\begin{align*}P(A)&=P(B_1)P(A|B_1)+P(B_2)P(A|B_2)+P(B_3)P(A|B_3)\\&=0.36\times0.2 + 0.41\times0.6 + 0.14\times1\\&=0.072 + 0.246 + 0.14\\&=0.458\end{align*}$