函数=overline (A)(B+overline (C)cdot overline (DE)) 的反函数是-|||-__ __( )A、=overline (A)(B+overline (C)cdot overline (DE)) 的反函数是-|||-__ __B、=overline (A)(B+overline (C)cdot overline (DE)) 的反函数是-|||-__ __C、=overline (A)(B+overline (C)cdot overline (DE)) 的反函数是-|||-__ __D、=overline (A)(B+overline (C)cdot overline (DE)) 的反函数是-|||-__ __
函数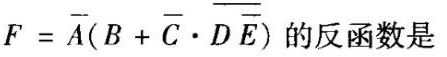 ( )
( )
- A、
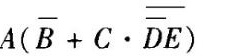
- B、
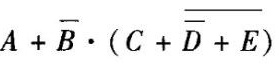
- C、
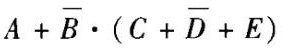
- D、
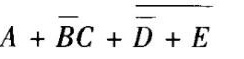
题目解答
答案
解析
反函数的求解需要掌握德摩根定律的应用。原函数$F$的反函数$F'$是将$F$的输出取反,即$F' = \overline{F}$。解题的关键步骤如下:
- 分解原函数结构:原式$F = \overline{A}(B + \overline{C} \cdot \overline{DE})$由两个因子组成,分别是$\overline{A}$和括号内的部分。
- 应用德摩根定律:对整个表达式取反时,将与($\cdot$)和或($+$)互换,并对每个变量取反。
- 逐层展开括号:特别注意运算优先级,确保每一步变形符合逻辑运算规则。
步骤1:对原函数取反
原函数为:
$F = \overline{A}(B + \overline{C} \cdot \overline{DE})$
取反后:
$F' = \overline{F} = \overline{\overline{A} \cdot (B + \overline{C} \cdot \overline{DE})}$
步骤2:应用德摩根定律
根据德摩根定律$\overline{XY} = \overline{X} + \overline{Y}$,展开得:
$F' = \overline{\overline{A}} + \overline{(B + \overline{C} \cdot \overline{DE})}$
步骤3:简化第一项
$\overline{\overline{A}} = A$,因此:
$F' = A + \overline{(B + \overline{C} \cdot \overline{DE})}$
步骤4:处理括号内的部分
对$\overline{(B + \overline{C} \cdot \overline{DE})}$再次应用德摩根定律:
$\overline{(B + \overline{C} \cdot \overline{DE})} = \overline{B} \cdot \overline{\overline{C} \cdot \overline{DE}}$
步骤5:展开内部乘积的反
对$\overline{\overline{C} \cdot \overline{DE}}$应用德摩根定律:
$\overline{\overline{C} \cdot \overline{DE}} = C + \overline{\overline{DE}} = C + D + E$
步骤6:整合所有部分
将所有步骤代入,最终得到:
$F' = A + \overline{B} \cdot (C + D + E)$
选项匹配
对比选项,B选项为$A + \overline{B} \cdot (C + \overline{D} + E)$,与推导结果一致。