2.已知 lim _(xarrow 1)dfrac ({x)^2+ax+b}(1-x)=1, 求常数a与b的值..
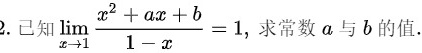 .
.
题目解答
答案
设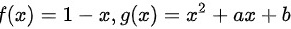
因为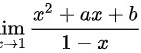
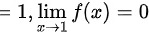 所以\
所以\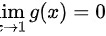
所以1+a+b=0
所以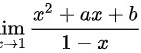
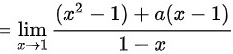
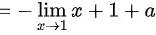
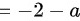
所以a=-3,b=2
解析
考查要点:本题主要考查极限的计算,特别是分式极限在分母趋近于0时的处理方法,以及如何通过极限存在性条件确定参数的值。
解题核心思路:
- 极限存在的条件:当分母趋近于0时,若极限存在且为有限值,则分子也必须趋近于0,否则极限会趋向无穷大或不存在。
- 分解分子:将分子拆分为与分母相关联的因式,通过约分简化表达式,进而求出参数。
- 代数方程联立:利用分子在特定点的值为0和极限值的条件,建立方程组求解参数。
破题关键点:
- 分子在$x=1$处的值为0,即$1 + a + b = 0$。
- 化简分式:通过分解分子,将分式转化为可约分的形式,从而求出极限表达式。
步骤1:确定分子在$x=1$处的值为0
因为分母$\lim_{x \to 1} (1 - x) = 0$,而极限$\lim_{x \to 1} \frac{x^2 + ax + b}{1 - x} = 1$存在,所以分子在$x=1$处的值也必须为0:
$1^2 + a \cdot 1 + b = 0 \implies 1 + a + b = 0.$
步骤2:分解分子并化简分式
将分子$x^2 + ax + b$拆分为$(x^2 - 1) + a(x - 1)$,则分式可表示为:
$\frac{x^2 + ax + b}{1 - x} = \frac{(x^2 - 1) + a(x - 1)}{1 - x} = \frac{(x - 1)(x + 1) + a(x - 1)}{1 - x}.$
提取公因式$(x - 1)$并约分:
$\frac{(x - 1)(x + 1 + a)}{1 - x} = -\frac{(x - 1)(x + 1 + a)}{x - 1} = -(x + 1 + a).$
步骤3:求极限并解方程
当$x \to 1$时,化简后的表达式极限为:
$\lim_{x \to 1} -(x + 1 + a) = -(1 + 1 + a) = - (2 + a).$
根据题意,该极限等于1,因此:
$- (2 + a) = 1 \implies a = -3.$
将$a = -3$代入$1 + a + b = 0$,得:
$1 - 3 + b = 0 \implies b = 2.$