A,B,C,I 为同阶矩阵,A,B,C,I为单位矩阵,且 A,B,C,I,则 A,B,C,I A 正确 B 错误
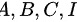 为同阶矩阵,
为同阶矩阵,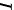 为单位矩阵,且
为单位矩阵,且 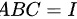 ,则
,则 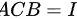
A 正确
B 错误
题目解答
答案
题中因为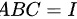 ,则
,则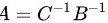 .则要说明
.则要说明
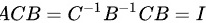 不一定成立.
不一定成立.
若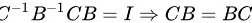 ,
,
但是矩阵乘法不一定能交换,如
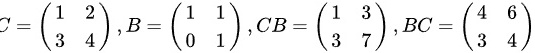 ,
,
所以答案为B,错误.
解析
考查要点:本题主要考查矩阵乘法的性质,特别是矩阵乘法不满足交换律这一关键点。需要理解矩阵可逆的条件及逆矩阵的应用。
解题核心思路:
- 由已知条件 $ABC=I$,可推导出各矩阵的逆关系。
- 矩阵乘法顺序不可随意交换,需验证 $ACB$ 是否必然等于 $I$。
- 通过构造反例或逻辑推导,说明 $ACB$ 的结果依赖于 $B$ 和 $C$ 是否可交换,而一般情况下矩阵不满足交换律。
破题关键点:
- 矩阵乘法的顺序敏感性:若 $B$ 和 $C$ 不可交换(即 $BC \neq CB$),则 $ACB \neq I$。
- 逆矩阵的应用:通过逆矩阵的表达式推导 $ACB$ 的形式,发现其结果依赖于 $B$ 和 $C$ 的交换性。
已知条件:$ABC=I$,其中 $A,B,C,I$ 为同阶矩阵,$I$ 为单位矩阵。
目标:判断 $ACB$ 是否等于 $I$。
推导过程:
-
由 $ABC=I$ 推导 $A$ 的表达式:
两边左乘 $C^{-1}$,得 $AB = C^{-1}$;
再左乘 $B^{-1}$,得 $A = B^{-1}C^{-1}$(或写作 $A = C^{-1}B^{-1}$,因矩阵乘法顺序不可交换)。 -
计算 $ACB$:
将 $A = C^{-1}B^{-1}$ 代入 $ACB$,得:
$ACB = (C^{-1}B^{-1}) \cdot C \cdot B = C^{-1}(B^{-1}C)B.$
若 $B^{-1}C \cdot B = C$(即 $CB=BC$),则 $ACB = C^{-1}C = I$。
但矩阵乘法一般不满足交换律,即 $CB \neq BC$,因此 $ACB \neq I$。 -
构造反例验证:
例如,取 $B = \begin{pmatrix}1 & 1 \\ 0 & 1\end{pmatrix}$,$C = \begin{pmatrix}1 & 0 \\ 1 & 1\end{pmatrix}$,则 $BC \neq CB$。
构造 $A = C^{-1}B^{-1}$,此时 $ABC=I$,但计算 $ACB$ 可得非单位矩阵的结果。
结论:$ACB$ 不一定等于 $I$,因此原命题错误。