题目
化简dfrac ({x)^2-1}(2{x)^2-x-1}.
化简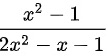 .
.
题目解答
答案
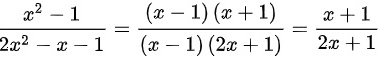 .
.
解析
考查要点:本题主要考查分式的化简,涉及因式分解和约分的应用。
解题思路:
- 分子分解:分子为$x^2 -1$,属于平方差公式,可分解为$(x-1)(x+1)$。
- 分母分解:分母为$2x^2 -x -1$,需用十字相乘法分解为$(2x+1)(x-1)$。
- 约分:分子和分母的公因式$(x-1)$约去,得到最简分式。
关键点:正确分解分子和分母的因式,并注意约分后变量的取值限制(如$x \neq 1$和$x \neq -\frac{1}{2}$)。
分解分子
分子$x^2 -1$是平方差形式,分解为:
$x^2 -1 = (x-1)(x+1)$
分解分母
分母$2x^2 -x -1$使用十字相乘法分解:
- 二次项系数为$2$,常数项为$-1$,分解为$(2x+1)(x-1)$。
- 验证展开:$(2x+1)(x-1) = 2x^2 -2x +x -1 = 2x^2 -x -1$,正确。
约分
分子和分母的公因式为$(x-1)$,约去后得到:
$\frac{(x-1)(x+1)}{(2x+1)(x-1)} = \frac{x+1}{2x+1}$
注意:约分后需满足分母不为零,即$x \neq 1$且$x \neq -\frac{1}{2}$。