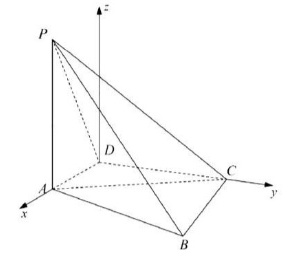
17.如图,四棱锥 P-ABCD 中, bot 底面ABCD, PA=AC=2 =1 , =sqrt (3).-|||-(1)若 bot PB, 证明: ykparallel 平面PBC;-|||-(2)若 bot DC, 且二面角 A-CP-D 的正弦值为 √42/7, 求AD.-|||-P-|||-D-|||-C-|||-A-|||-B

1. 【答案】

证明：$\because PA\bot 面ABCD$，$AD\subset 面ABCD$。

$\therefore PA\bot AD$。又$\because AD\bot PB$，$PA\cap PB=P$, $PA,PB\subset $面$PAB$

$\therefore AD\bot 面PAB$，$\because AB\subset 面PAB$，$\therefore AD\bot AB$

又$\because AB=\sqrt{3}$，$BC=1$，$AC=2$，$\therefore {AB}^{2}+{BC}^{2}={AC}^{2}$

$\therefore BC\bot AB$，又$BC，AD\subset 面ABCD$，$\therefore AD\ykparallel BC$，又$\because AD\not\subset 面PBC$，$BC\subset 面PBC$。

$\therefore AD\ykparallel 面PBC$。

2. 【答案】

过D点作$Dz\ykparallel PA$。

分别以DA，DC，Dz为x，y，z轴，建立空间直角坐标系，设$AD=a$，则$DC=\sqrt {4-{a}^{2}}$

$\therefore D(0，0，0)$，$A\left(a，0，0\right)$，$C(0，\sqrt {4-{a}^{2}}，0)$，$P\left(a，0，2\right)$

$\therefore \overrightarrow{DC}=\left(0，\sqrt{4-{a}^{2}}，0\right)$，$\overrightarrow {DP}=(a，0，2)$

设面DCP的一个法向量$\overrightarrow {{n}_{1}}=({x}_{1}，{y}_{1}，{z}_{1})$，$\therefore \left\{\begin{array}{l}\sqrt{4-{a}^{2}}\cdot {y}_{1}=0\\ a{x}_{1}+2{z}_{1}=0\end{array}\right.$

取${x}_{1}=2$，$\therefore \overrightarrow{{n}_{1}}=(2，0，-a)$

$\therefore \overrightarrow {AP}=(0，0，2)$，$\overrightarrow {AC}=(-a，\sqrt {4-{a}^{2}}，0)$

设面ACP的一个法向量$\overrightarrow {{n}_{2}}=({x}_{2}，{y}_{2}，{z}_{2})$，

$\therefore \left\{\begin{array}{l}2{z}_{2}=0\\ -a{x}_{2}+\sqrt{4-{a}^{2}}{y}_{2}=0\end{array}\right.$

取${y}_{2}=a$

$\therefore \overrightarrow{{n}_{2}}=\left(\sqrt{4-{a}^{2}}，a，0\right)$

$\because $二面角$A-CP-D$的正弦值为$\dfrac {\sqrt {42}}{7}$

$\therefore $余弦值的绝对值为$\dfrac {1}{\sqrt {7}}$。

$\therefore \left|\cos \theta \right|=\dfrac{1}{\sqrt{7}}=\left|\dfrac{\overrightarrow{{n}_{1}}\cdot \overrightarrow{{n}_{2}}}{|\overrightarrow{{n}_{1}}|\cdot |\overrightarrow{{n}_{2}}|}\right|=\dfrac{2\sqrt{4-{a}^{2}}}{\sqrt{4+{a}^{2}}\cdot 2}$

$\therefore {a}^{2}=3$，$\therefore a=\sqrt {3}$

$\therefore AD=\sqrt {3}$。