题目
计算积分,其中C是从0到1+i的直线段(int )_(C)(x-y+i(x)^2)dz
计算积分,其中C是从0到1+i的直线段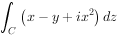
题目解答
答案
A
解析
考查要点:本题主要考查复变函数沿直线段的积分计算,需要掌握参数方程的建立、微分dz的表达式以及积分的展开与计算。
解题核心思路:
- 参数化积分路径:将直线段C表示为参数方程,通常用参数$t \in [0,1]$表示从起点到终点的移动。
- 表达dz和被积函数:通过参数方程求出$dz$,并将被积函数中的$x$、$y$用参数$t$表示。
- 化简积分并计算:将复积分转化为关于$t$的实积分,展开后分项计算。
破题关键点:
- 正确参数化路径:直线段C的参数方程为$z(t) = (1+i)t$,对应$x = t$,$y = t$。
- 准确计算dz:$dz = (1+i)dt$。
- 代入被积函数:将$x - y + i x^2$代入参数化后的表达式,化简后积分转化为关于$t$的实积分。
参数化积分路径
直线段C从$0$到$1+i$,参数化为:
$z(t) = (1+i)t \quad (t \in [0,1])$
对应:
$x = t, \quad y = t$
计算dz
对$z(t)$求导:
$\frac{dz}{dt} = 1+i \quad \Rightarrow \quad dz = (1+i)dt$
代入被积函数
被积函数为:
$x - y + i x^2 = t - t + i t^2 = i t^2$
积分表达式
原积分转化为:
$\int_{C} (x - y + i x^2) dz = \int_{0}^{1} i t^2 \cdot (1+i) dt$
化简并计算
展开系数:
$i(1+i) = i + i^2 = i - 1$
积分变为:
$\int_{0}^{1} (i - 1) t^2 dt = (i - 1) \int_{0}^{1} t^2 dt = (i - 1) \cdot \frac{1}{3} = \frac{-1 + i}{3}$