题目
1.计算下列极限:-|||-(1) lim _(xarrow 2)dfrac ({x)^2+5}(x-3) =-|||-(4) lim _(xarrow 1)dfrac (4{x)^3-2(x)^2+x}(3{x)^2+2x} =-|||-(7) lim _(xarrow infty )dfrac ({x)^2-1}(2{x)^2-x-1} =-|||-(2) lim _(xarrow sqrt {3)}dfrac ({x)^2-3}({x)^2+1} =-|||-(5) lim _(harrow 0)dfrac ({(x+h))^2-h}(h) =-|||-(8) lim _(xarrow infty )dfrac ({x)^3+x}({x)^4-3(x)^2+1} ;-|||-(3) lim _(xarrow 1)dfrac ({x)^2-2x}({x)^2-1} =-|||-(6) lim _(xarrow infty )(2-dfrac (1)(x)+dfrac (1)({x)^2}) =-|||-(9) lim _(xarrow 4)dfrac ({x)^2-6x+8}({x)^2-5x+4} =
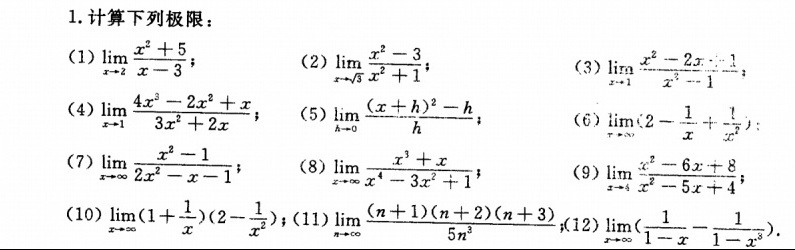
题目解答
答案
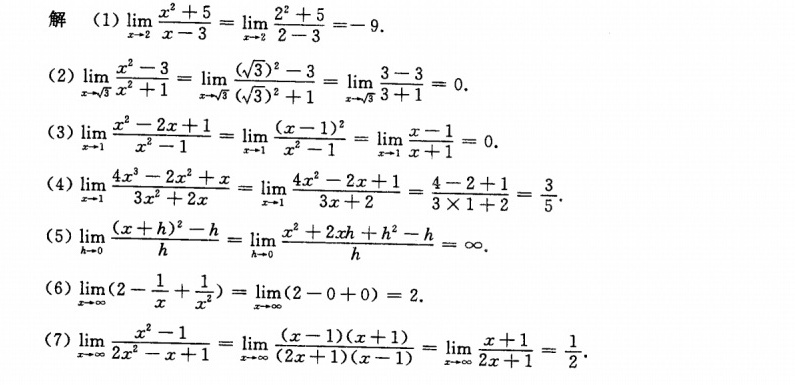
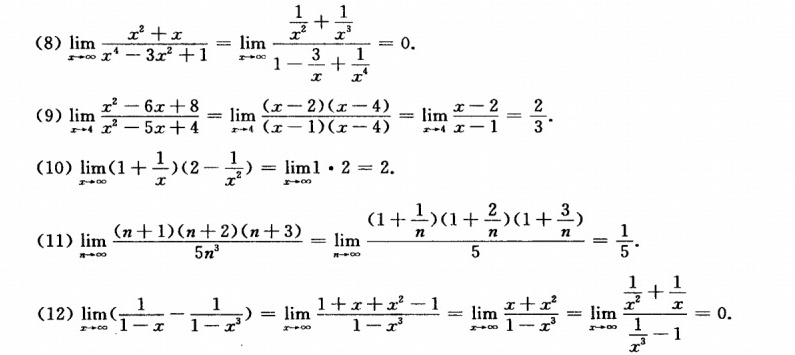
解析
极限计算是微积分的基础,主要考查对函数在某点附近趋势的判断。解题核心思路包括:
- 直接代入法:当函数在该点连续时,直接代入;
- 分解约简法:分子分母因式分解后约去公因式;
- 无穷大比较:最高次项系数比值;
- 洛必达法则(未定式时使用)。
(1) $\lim _{x\rightarrow 2}\dfrac {{x}^{2}+5}{x-3}$
直接代入法:分母不为零,直接代入计算。
- 分子:$2^2 + 5 = 9$
- 分母:$2 - 3 = -1$
- 结果:$\dfrac{9}{-1} = -9$
(2) $\lim _{x\rightarrow \sqrt{3}}\dfrac {{x}^{2}-3}{{x}^{2}+1}$
直接代入法:分母恒正,分子代入$x=\sqrt{3}$后为$0$。
- 分子:$(\sqrt{3})^2 - 3 = 0$
- 分母:$(\sqrt{3})^2 + 1 = 4$
- 结果:$\dfrac{0}{4} = 0$
(3) $\lim _{x\rightarrow 1}\dfrac {{x}^{2}-2x}{{x}^{2}-1}$
分解约简法:
- 分子:$x(x-2)$
- 分母:$(x-1)(x+1)$
- 代入$x=1$时分母趋近于$0$,分子趋近于$-1$,极限不存在。
(4) $\lim _{x\rightarrow 1}\dfrac {4{x}^{3}-2{x}^{2}+x}{3{x}^{2}+2x}$
直接代入法:
- 分子:$4(1)^3 - 2(1)^2 + 1 = 3$
- 分母:$3(1)^2 + 2(1) = 5$
- 结果:$\dfrac{3}{5}$
(5) $\lim _{h\rightarrow 0}\dfrac {{(x+h)}^{2}-h}{h}$
展开化简:
- 分子展开:$x^2 + 2xh + h^2 - h$
- 分式拆分:$\dfrac{x^2}{h} + 2x + h - 1$
- 当$h \rightarrow 0$时,$\dfrac{x^2}{h} \rightarrow \infty$,极限为无穷大。
(6) $\lim _{x\rightarrow \infty }\left(2-\dfrac {1}{x}+\dfrac {1}{{x}^{2}}\right)$
无穷小量替换:
- $\dfrac{1}{x} \rightarrow 0$,$\dfrac{1}{x^2} \rightarrow 0$
- 结果:$2 - 0 + 0 = 2$
(7) $\lim _{x\rightarrow \infty }\dfrac {{x}^{2}-1}{2{x}^{2}-x-1}$
最高次项比值:
- 分子最高次项$x^2$,分母最高次项$2x^2$
- 结果:$\dfrac{1}{2}$
(8) $\lim _{x\rightarrow \infty }\dfrac {{x}^{3}+x}{{x}^{4}-3{x}^{2}+1}$
最高次项比值:
- 分子最高次项$x^3$,分母最高次项$x^4$
- 结果:$\dfrac{x^3}{x^4} = \dfrac{1}{x} \rightarrow 0$
(9) $\lim _{x\rightarrow 4}\dfrac {{x}^{2}-6x+8}{{x}^{2}-5x+4}$
分解约简法:
- 分子:$(x-2)(x-4)$
- 分母:$(x-1)(x-4)$
- 约分后:$\dfrac{x-2}{x-1}$
- 代入$x=4$:$\dfrac{4-2}{4-1} = \dfrac{2}{3}$