题目
9.设函数 (x)=dfrac (1)(x) , (x)=1-x, 则 [ g(x)] = __-|||-A. https:/img.zuoyebang.cc/zyb_28ef82914cba21022739e1da900e4cb3.jpg-dfrac (1)(x) B. https:/img.zuoyebang.cc/zyb_28ef82914cba21022739e1da900e4cb3.jpg+dfrac (1)(x) C. dfrac (1)(1-x) D.x
题目解答
答案
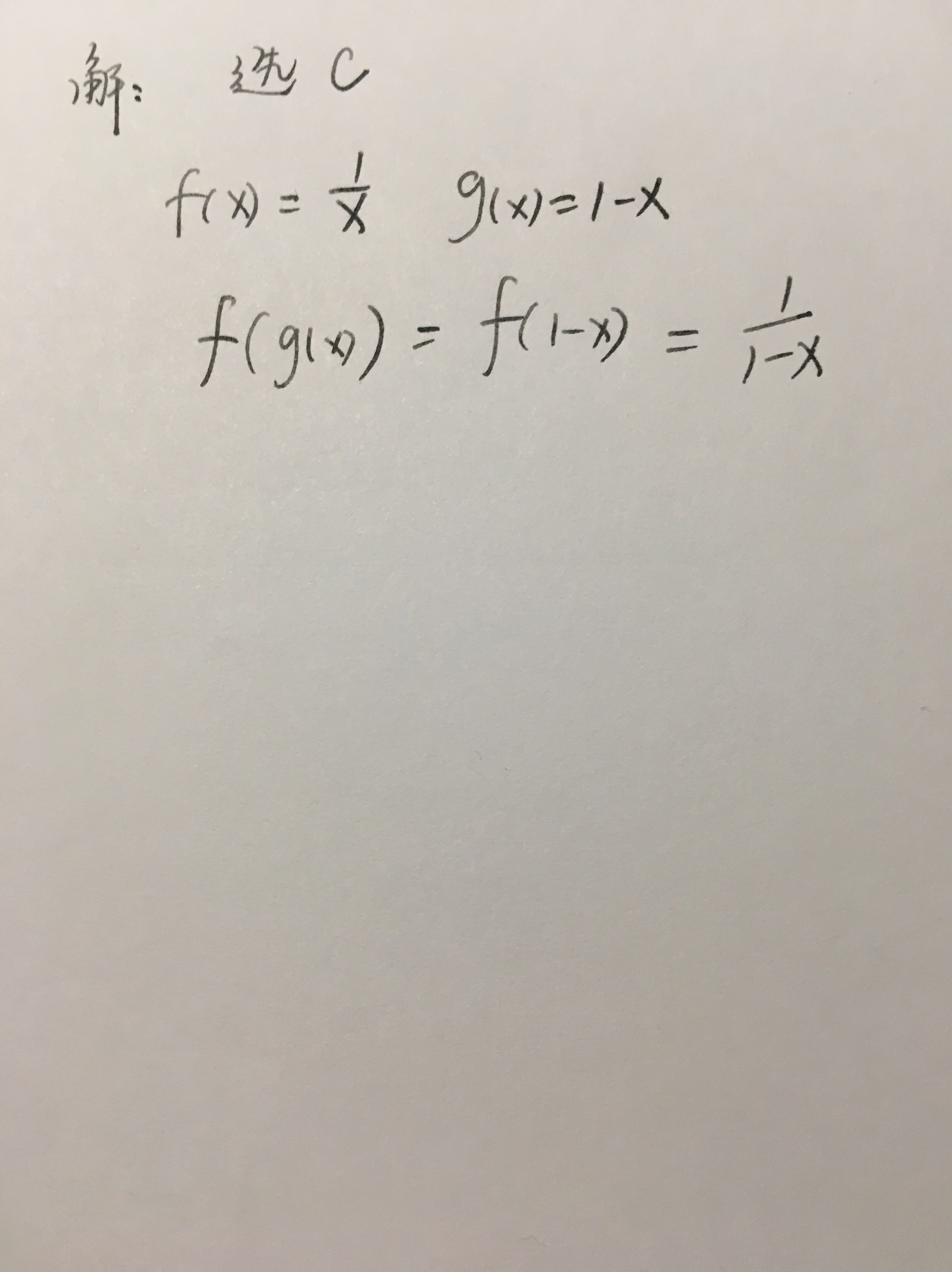
解析
考查要点:本题主要考查复合函数的概念及代入求值的能力。
解题思路:复合函数$f(g(x))$的求解需要先计算内层函数$g(x)$的值,再将其结果作为外层函数$f$的输入。
关键点:正确代入并化简表达式,注意分母的符号和形式。
步骤1:确定内层函数的值
已知$g(x) = 1 - x$,因此内层函数的输出为$1 - x$。
步骤2:将内层函数结果代入外层函数
外层函数$f(x) = \dfrac{1}{x}$,因此$f(g(x)) = f(1 - x) = \dfrac{1}{1 - x}$。
选项分析:
- 选项C $\dfrac{1}{1 - x}$ 与计算结果一致,为正确答案。