阅读材料4.对数的创始人是苏格兰数学家纳皮尔(J.Napier,1550−1617),1614年,纳皮尔出版了《奇妙的对数》,在前言里,纳皮尔告诉我们他发明对数的动机;没有什么比大数的乘、除、开平方或开立方运算更让数学工作者头痛、更阻碍计算者了,这不仅浪费时间,而且容易出错是,因此,我开始考虑怎样消除这些障碍,经过长时间的思索,我终于找到了一些漂亮的简短法则⋯⋯对数b=logam是实数,其中b,a,m的关系是m=ab,对数具有一种奇妙的性质:可以把高一级的乘、除、乘方、开方运算分别转化为低一级的加、减、乘、除运算.进行大量的计算时,对数的这种功能可使计算的效率成倍地提高.比如计算264的近似值,若用64个2连乘,其繁琐与费时可以想象,如果利用对数的定义和运算公式,可以操作如下:因为lg264=64⋅lg2≈64×0.3010=19.2640,再利用对数表查表规则,查出0.2640≈lg1.836,于是19.2640=0.2640+19=lg1.836+19=lg(1.836×1019),可得264的近似值为1.836×1019,就可以体会到对数的数字计算上的优越性!请依据上述材料,完成下列问题:写出你知道的对数运算公式(至少3个).利用阅读材料4,计算log25的近似值;(计算过程精确到0.0001,结果精确到0.01).利用阅读材料4提供的思想和方法计算3√3472的近似值.(计算过程精确到0.0001,结果精确到0.01).附件.对数用表(部分及查表说明)一、使用说明1.整数部分是一位非零数字.lg2.573:在第1列找25再横行找“7”为4099,修正值“3”为5.所以lg2.573≈0.4099+0.0005=0.4104.2.整数部分不是一位非零数字的.用科学记数法表示N×10n.lg25730=lg(2.573×104)=lg2.573+4=4.4104lg0.222573=lg(2.573×10−3)=lg2.573+(−3)=−2.5896.3.查反对数时,正小数部分查表,整数部分决定小数点的位置.6.4104:由0.4104查出0.4104=lg2.573.则6.4104=lg2.573+6=lg(2.573×106)=lg2573000.负的对数化负整数+正纯小数,再同样查.二、对数用表(部分)log 0 1 2 3 4 5 6 7 8 9 表尾差(修正值)-|||-1 2 3 4 5 6 7 8 9-|||-15 1761 1790 1818 1847 1875 1903 1931 1959 1987 2014 3 6 8 11 14 17 20 21 25-|||-16 2041 2068 2095 2122 2148 2175 2201 2227 2253 2279 3 5 6 11 13 16 18 21 24-|||-17 2304 2330 2355 2380 2405 2430 2455 2480 2504 2529 2 5 7 10 12 15 17 20 22-|||-18 2553 2577 2601 2625 2648 2672 2695 2718 2742 2765 2 5 7 9 12 416 19 21-|||-19 2788 2810 2833 2856 2878 2900 2923 2945 2967 2989 2 4 7 9 11 13 6 18 20-|||-20 3010 3032 3054 3075 3096 3118 3139 3160 3181 3201 2 4 6 8 11 13 517 19-|||-21 3222 3243 3263 3284 3304 3324 3345 3365 3385 3404 2 4 6 8 0 214 6 8-|||-22 3424 3444 3464 3483 3502 3522 3541 3560 3579 3598 2 4 6 8 012 13 15 17-|||-23 3617 3636 3655 3674 3692 3711 3729 3747 3766 3784 2 4 6 7 9 11 3 517-|||-24 3802 3820 3838 3856 3874 3892 3909 3927 3945 3962 2 4 6 7 9 11 2 4 6-|||-5 3979 3997 4014 4031 4048 4065 4082 4099 4116 4133 2 3 5 7 9 0 415-|||-6 4150 4166 4183 4200 4216 4232 4249 4265 4281 4298 2 3 5 7 8 012/11 315-|||-27 4314 4330 4346 4362 4378 4393 4409 4425 4440 4456 2 3 5 6 8 9 11 3 14-|||-28 4472 4487 4502 4518 4533 4548 4564 4579 4594 4609 2 3 5 6 8 9 11 2 4-|||-9 4624 4639 4654 4669 4683 4698 4713 4728 4742 4557 1 3 4 6 7 9 0 2| 13-|||-30 4771 4786 4800 4814 4829 4843 4857 4871 4886 4900 1 3 4 6 7 9 011 13-|||-31 4914 4928 4942 4955 4969 4983 3997 5011 5024 5038 1 3 4 6 7 8 011 12-|||-32 5051 5065 5079 5092 5105 5119 5132 5145 5159 5172 1 3 4 5 7 8 9 11 12-|||-33 5185 5198 5211 5224 5237 5250 5263 5276 5289 5302 1 3 4 5 6 8 9 012-|||-34 5315 5328 5340 5353 5366 5378 5391 5403 5416 5428 1 3 4 5 6 8 9 9 11/11-|||-35 5441 6453 5465 5478 5490 5502 5514 5527 5539 5551 1 2 4 5 6 7 9 0-|||-36 5563 5575 5587 5599 5611 5623 5635 5647 5658 5670 1 2 4 5 6 7 8 0 11-|||-37 5682 5694 4705 5717 5729 5740 5752 5763 5775 5986 1 2 3 5 6 7 8 9 10-|||-38 5798 5809 5821 5832 5843 5855 5866 5877 5888 5899 1 2 3 5 6 7 8 9 0-|||-39 5911 5922 5933 5944 5955 5966 5977 5988 5999 6010 1 2 3 4 5 7 8 9 0-|||-40 6021 6031 6042 6053 6064 6075 6085 6096 6107 6117 1 2 3 4 5 6 7 9 10
阅读材料4.对数的创始人是苏格兰数学家纳皮尔(J.Napier,1550−1617),1614年,纳皮尔出版了《奇妙的对数》,在前言里,纳皮尔告诉我们他发明对数的动机;没有什么比大数的乘、除、开平方或开立方运算更让数学工作者头痛、更阻碍计算者了,这不仅浪费时间,而且容易出错是,因此,我开始考虑怎样消除这些障碍,经过长时间的思索,我终于找到了一些漂亮的简短法则⋯⋯
对数b=logam是实数,其中b,a,m的关系是m=ab,对数具有一种奇妙的性质:可以把高一级的乘、除、乘方、开方运算分别转化为低一级的加、减、乘、除运算.进行大量的计算时,对数的这种功能可使计算的效率成倍地提高.
比如计算264的近似值,若用64个2连乘,其繁琐与费时可以想象,如果利用对数的定义和运算公式,可以操作如下:
因为lg264=64⋅lg2≈64×0.3010=19.2640,再利用对数表查表规则,查出
0.2640≈lg1.836,于是19.2640=0.2640+19=lg1.836+19=lg(1.836×1019),
可得264的近似值为1.836×1019,就可以体会到对数的数字计算上的优越性!
请依据上述材料,完成下列问题:
写出你知道的对数运算公式(至少3个).
利用阅读材料4,计算log25的近似值;(计算过程精确到0.0001,结果精确到0.01).
利用阅读材料4提供的思想和方法计算3√3472的近似值.(计算过程精确到0.0001,结果精确到0.01).
附件.对数用表(部分及查表说明)
一、使用说明
1.整数部分是一位非零数字.
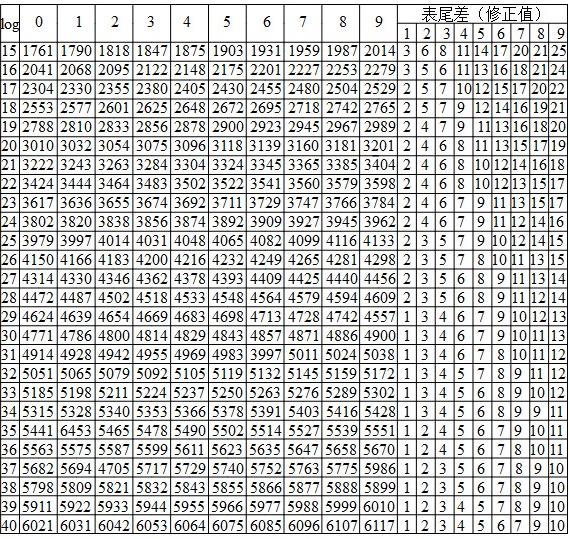
lg2.573:在第1列找25再横行找“7”为4099,修正值“3”为5.
所以lg2.573≈0.4099+0.0005=0.4104.
2.整数部分不是一位非零数字的.用科学记数法表示N×10n.
lg25730=lg(2.573×104)=lg2.573+4=4.4104
lg0.222573=lg(2.573×10−3)=lg2.573+(−3)=−2.5896.
3.查反对数时,正小数部分查表,整数部分决定小数点的位置.
6.4104:由0.4104查出0.4104=lg2.573.
则6.4104=lg2.573+6=lg(2.573×106)=lg2573000.
负的对数化负整数+正纯小数,再同样查.
二、对数用表(部分)
题目解答
答案
- (1)
;
;
.
- (2)
.
- (3)
.