2.设随机变量X的密度函数为 f(x)= )=dfrac {7)(8)-|||-求:(1)常数a,b (2) (dfrac (1)(2)lt Xlt dfrac (3)(2))-|||-(3)X的分布函数F (x)
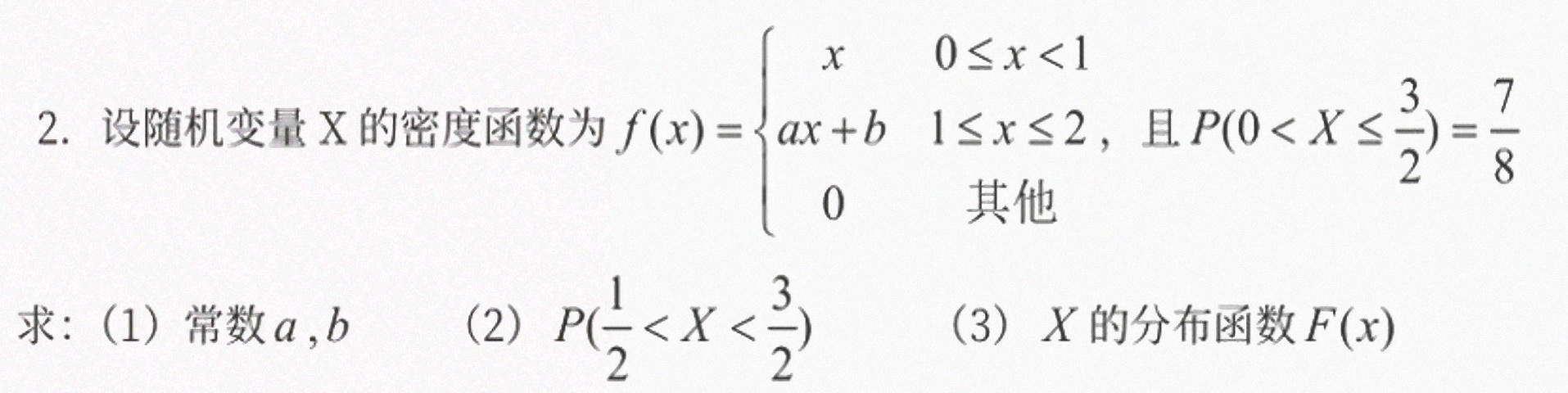
题目解答
答案

解析
考查要点:本题主要考查连续型随机变量的密度函数性质、概率计算及分布函数的求解。
解题思路:
- 利用密度函数的归一性(积分等于1)和题目给出的概率条件,建立方程组求解常数$a$和$b$。
- 分段积分计算指定区间的概率。
- 分段积分求分布函数,注意不同区间的表达式衔接。
关键点:
- 密度函数的归一性:$\int_{-\infty}^{+\infty} f(x)dx = 1$。
- 分布函数$F(x)$是密度函数的变上限积分,需分段讨论。
(1) 求常数$a$和$b$
步骤1:归一性方程
密度函数积分等于1:
$\int_{0}^{1} x dx + \int_{1}^{2} (ax + b) dx = 1$
计算得:
$\left[ \frac{1}{2}x^2 \right]_0^1 + \left[ \frac{a}{2}x^2 + b x \right]_1^2 = \frac{1}{2} + \left( \frac{a}{2}(4-1) + b(2-1) \right) = \frac{1}{2} + \frac{3a}{2} + b = 1$
整理得方程:
$\frac{3a}{2} + b = \frac{1}{2} \quad (1)$
步骤2:利用概率条件
已知$P(0 < X \leq \frac{3}{2}) = \frac{7}{8}$,分段积分:
$\int_{0}^{1} x dx + \int_{1}^{\frac{3}{2}} (ax + b) dx = \frac{7}{8}$
计算得:
$\left[ \frac{1}{2}x^2 \right]_0^1 + \left[ \frac{a}{2}x^2 + b x \right]_1^{\frac{3}{2}} = \frac{1}{2} + \left( \frac{a}{2} \cdot \frac{5}{4} + b \cdot \frac{1}{2} \right) = \frac{1}{2} + \frac{5a}{8} + \frac{b}{2} = \frac{7}{8}$
整理得方程:
$\frac{5a}{8} + \frac{b}{2} = \frac{3}{8} \quad (2)$
步骤3:解方程组
联立方程(1)和(2),解得:
$a = -1, \quad b = 2$
(2) 求$P\left( \frac{1}{2} < X < \frac{3}{2} \right)$
分段积分:
$\int_{\frac{1}{2}}^{1} x dx + \int_{1}^{\frac{3}{2}} (-x + 2) dx$
计算得:
$\left[ \frac{1}{2}x^2 \right]_{\frac{1}{2}}^1 + \left[ -\frac{1}{2}x^2 + 2x \right]_1^{\frac{3}{2}} = \frac{3}{4}$
(3) 求分布函数$F(x)$
分段讨论:
- 当$x < 0$时:$F(x) = 0$
- 当$0 \leq x < 1$时:
$F(x) = \int_{0}^{x} t dt = \frac{1}{2}x^2$ - 当$1 \leq x \leq 2$时:
$F(x) = \int_{0}^{1} t dt + \int_{1}^{x} (-t + 2) dt = \frac{1}{2} + \left( -\frac{1}{2}x^2 + 2x - \frac{3}{2} \right) = -\frac{1}{2}x^2 + 2x - 1$ - 当$x > 2$时:$F(x) = 1$