1.求下列极限:-|||-(1) lim _(xarrow 0)dfrac (sin 2x)(x);-|||-(3) lim _(xarrow dfrac {pi )(2)}dfrac (cos x)(x-dfrac {pi )(2)}-|||-(2) lim _(xarrow 0)dfrac (sin {x)^3}({(sin x))^2};-|||-(4) lim _(xarrow 0)dfrac (tan x)(x);1.求下列极限:-|||-(1) lim _(xarrow 0)dfrac (sin 2x)(x);-|||-(3) lim _(xarrow dfrac {pi )(2)}dfrac (cos x)(x-dfrac {pi )(2)}-|||-(2) lim _(xarrow 0)dfrac (sin {x)^3}({(sin x))^2};-|||-(4) lim _(xarrow 0)dfrac (tan x)(x);
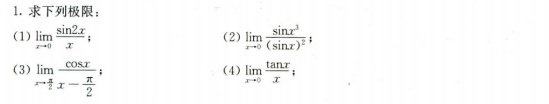
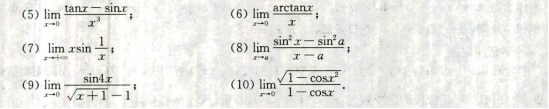
题目解答
答案


解析
本题主要考查利用重要极限$\lim _{x\rightarrow 0}\frac{\sin x}{x}=1$及函数极限的运算法则求解极限,具体分析如下:
(1) $\lim _{x\rightarrow 0}\frac{\sin 2x}{x}$
利用重要极限$\lim _{t\rightarrow 0}\frac{\sin t}{t}=1$,令$t=2x$,则:
$\lim _{x\rightarrow 0}\frac{\sin 2x}{x}=2\lim _{x\rightarrow 0}\frac{\sin 2x}{2x}=2\times1=2$
(2) $\lim _{x\rightarrow 0}\frac{\sin x^3}{(\sin x)^2}$
当$x\rightarrow0$时,$\sin x\sim x$,$\sin x^3\sim x^3$,则:
$\lim _{x\rightarrow 0}\frac{\sin x^3}{(\sin x)^2}\sim\lim _{x\rightarrow 0}\frac{x^3}{x^2}=\lim _{x\rightarrow 0}x=0$
(3) $\lim _{x\rightarrow \frac{\pi }{2}}\frac{\cos x}{x-\frac{\pi }{2}}$
令$t=x-\frac{\pi }{2}$,则$x=t+\frac{\pi }{2}$,当$x\rightarrow\frac{\pi }{2}$时$t\rightarrow0$,且$\cos x=\cos\left(t+\frac{\pi }{2}\right)=-\sin t$,则:
$\lim _{t\rightarrow 0}\frac{-\sin t}{t}=-\lim _{t\rightarrow 0}\frac{\sin t}{t}=-1$
(4) $\lim _{x\rightarrow 0}\frac{\tan x}{x}$
$\tan x=\frac{\sin x}{\cos x}$,则:
$\lim _{x\rightarrow 0}\frac{\tan x}{x}=\lim _{x\rightarrow 0}\frac{\sin x}{x}\cdot\frac{1}{\cos x}=1\times1=1$
(5) $\lim _{x\rightarrow 0}\frac{\tan x-\sin x}{x^3}$
化简分子:$\tan x-\sin x=\frac{\sin x}{\cos x}-\sin x=\sin x\left(\frac{1-\cos x}{\cos x}\right)$,利用$1-\cos x=2\sin^2\frac{x}{2}$,则:
$\lim _{x\rightarrow 0}\frac{\sin x(1-\cos x)}{x^3\cos x}=\lim _{x\rightarrow 0}\frac{\sin x}{x}\cdot\frac{2\sin^2\frac{x}{2}}{x^2}\cdot\frac{1}{\cos x}=1\cdot\frac{1}{2}\cdot1=\frac{1}{2}$
(6) $\lim _{x\rightarrow 0}\frac{\arctan x}{x}$
令$t=\arctan x$,则$x=\tan t$,当$x\rightarrow0$时$t\rightarrow0$,则:
$\lim _{t\rightarrow 0}\frac{t}{\tan t}=\lim _{t\rightarrow 0}\frac{t}{\sin t}\cdot\cos t=1\times1=1$
(7) $\lim _{x\rightarrow +\infty }x\sin \frac{1}{x}$
令$t=\frac{1}{x}$,当$x\rightarrow+\infty$时$t\rightarrow0^+$,则:
$\lim _{t\rightarrow 0^+}\frac{\sin t}{t}=1$
(8) $\lim _{x\rightarrow a}\frac{\sin^2 x-\sin^2 a}{x-a}$
利用平方差公式:$\sin^2 x-\sin^2 a=(\sin x-\sin a)(\sin x+\sin a)$,再用和差化积:
$\sin x-\sin a=2\cos\frac{x+a}{2}\sin\frac{x-a}{2}$
则:
$\lim _{x\rightarrow a}\cos\frac{x+a}{2}\cdot\frac{\sin\frac{x-a}{2}}{\frac{x-a}{2}}\cdot(\sin x+\sin a)=\cos a\cdot1\cdot2\sin a=\sin 2a$
(9) $\lim _{x\rightarrow 0}\frac{\sin 4x}{\sqrt{x+1}-1}$
分母有理化:$\sqrt{x+1}-1=\frac{x}{\sqrt{x+1}+1}$,则:
$\lim _{x\rightarrow 0}\frac{\sin 4x}{x}\cdot(\sqrt{x+1}+1)=4\times2=8$
(10) $\lim _{x\rightarrow 0}\frac{\sqrt{1-\cos x^2}}{1-\cos x}$
利用$1-\cos t=2\sin^2\frac{t}{2}$,则:
$\sqrt{1-\cos x^2}=\sqrt{2}\left|\sin\frac{x^2}{2}\right|\approx\sqrt{2}\cdot\frac{x^2}{2}\quad(1-\cos x\approx\frac{x^2}{2})$
$\lim _{x\rightarrow 0}\frac{\sqrt{2}\cdot\frac{x^2}{2}}{\frac{x^2}{2}}=\sqrt{2}$