题目
设 P ( A ) = 0.3 , (Acup B)=0.8,若 A 与 B 互斥则 P ( B - A ) = ( ) 。A 0.7B 0.5C 0.4D 0.3
设 P ( A ) = 0.3 , 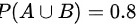 ,若 A 与 B 互斥则 P ( B - A ) = ( ) 。
,若 A 与 B 互斥则 P ( B - A ) = ( ) 。
A 0.7
B 0.5
C 0.4
D 0.3
题目解答
答案
解:选B。
已知 P ( A ) = 0.3 , 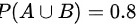 ,
,
∵A与B互斥
∴A与B不相交
∴ P ( B - A )
=P(B)
=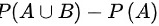
=0.8-0.3
=0.5
所以,若 A 与 B 互斥则 P ( B - A ) =0.5,本题选B。
解析
考查要点:本题主要考查互斥事件的概率性质及事件差集的概率计算。
解题核心思路:
- 互斥事件的性质:若事件$A$与$B$互斥,则$P(A \cup B) = P(A) + P(B)$,且$P(A \cap B) = 0$。
- 事件差集的含义:$B - A$表示“$B$发生但$A$不发生”,其概率可表示为$P(B - A) = P(B) - P(A \cap B)$。
- 关键推导:利用互斥条件简化公式,直接求出$P(B)$,再结合差集的定义得出结果。
步骤1:利用互斥事件性质求$P(B)$
已知$P(A \cup B) = 0.8$,且$A$与$B$互斥,根据公式:
$P(A \cup B) = P(A) + P(B)$
代入已知数据:
$0.8 = 0.3 + P(B) \implies P(B) = 0.8 - 0.3 = 0.5$
步骤2:计算$P(B - A)$
由于$A$与$B$互斥,$A \cap B = \emptyset$,因此:
$P(B - A) = P(B) - P(A \cap B) = P(B) - 0 = 0.5$