题目
1.已知函数f(x)的定义域为[0,1],则 ((x)^2-3) 的定义域为 )-|||-A.[0,1] B. [ sqrt (3),2] -|||-C. [ -2,-sqrt (3)] D. [ -2,-sqrt (3)] cup [ sqrt (3),2]
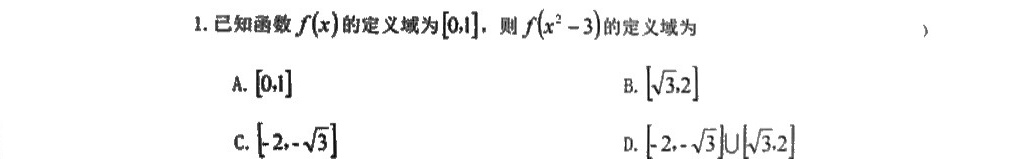
题目解答
答案

解析
本题考查抽象函数定义域的求解。函数定义域是指指自变量$x$的取值范围,对于函数$f(x)$,其定义域为$[0,1]$,即当$f$作用的对象在$[0,1])内时函数有意义。对于\(f(x^2 - 3)$,需要$x^2 - 3$这个整体落在$f(x)$的定义域$[0,1]$内,由此可列出不等式求解$xathbf{x}$的范围。
步骤1:根据函数定义域的定义列不等式
因为$f(x)$的定义域为$[0,1]),所以对于\(f(x^2 - 3)$,必须满足:
$0 \leq x^2 - 3 \leq 1$
步骤2:解不等式组
-
解$x^2 - 3 \geq 0$:
$x^2 \geq 3\implies x \geq \sqrt{3}\quad \text{或}\quad x \leq -\sqrt{3}$ -
解$x^2 - 3 \leq 1$:
$x^2 \leq 4\implies -2 \leq x \leq 2$
步骤3:求交集得到$x$的定义域
取上述两个不等式的交集:
- 当$x \geq \sqrt{3}$时,结合$-2 \leq x \leq 2)得\(\sqrt{3} \leq x \leq 2$;
- 当$x \leq -\sqrt{3}$时,结合$-2 \leq x \leq 2$得$-2 \leq x \leq -\sqrt{3}$。
综上,$f(x^2 - 3)$的定义域为$[-2, -\sqrt{3}] \cup [\sqrt{3}, 2]$。