题目
5.求由 =(x)^3 =2, y=0 所围成的图形,绕x轴旋转所得的旋转体的体积.

题目解答
答案
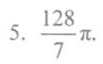
解析
考查要点:本题主要考查旋转体体积的计算,特别是利用圆盘法求解绕x轴旋转的体积问题。
解题核心思路:
- 确定积分区间:找出曲线$y=x^3$、直线$x=2$和$y=0$围成的区域在$x$轴上的投影范围,即$x$从$0$到$2$。
- 选择方法:由于旋转体为实心结构,使用圆盘法,其体积公式为$V = \pi \int_{a}^{b} [f(x)]^2 \, dx$。
- 代入计算:将$f(x) = x^3$代入公式,计算定积分即可。
破题关键点:
- 正确识别积分区间和被积函数。
- 明确圆盘法的适用条件及公式形式。
步骤1:确定积分区间
曲线$y=x^3$与$y=0$(x轴)的交点为$x=0$,与$x=2$的交点为$(2,8)$。因此,积分区间为$x \in [0, 2]$。
步骤2:应用圆盘法公式
每个垂直于x轴的截面为圆盘,半径$r = y = x^3$,体积元素为$dV = \pi r^2 dx = \pi (x^3)^2 dx = \pi x^6 dx$。
步骤3:计算定积分
$V = \pi \int_{0}^{2} x^6 \, dx = \pi \left[ \frac{x^7}{7} \right]_{0}^{2} = \pi \left( \frac{2^7}{7} - 0 \right) = \frac{128}{7} \pi.$