题目
设事件A,B相互独立,(Acup B)=0.7 P(A)=0.4,则(Acup B)=0.7 P(A)=0.4A.0.7B.0.6C.0.5D.0.4
设事件A,B相互独立,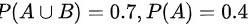 ,则
,则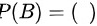
A.0.7
B.0.6
C.0.5
D.0.4
题目解答
答案
答案:C
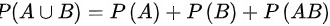
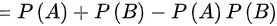
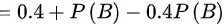
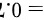
即可得出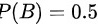
解析
考查要点:本题主要考查独立事件的概率计算以及概率加法公式的应用。
解题核心思路:
- 利用独立事件的性质:若事件A与B独立,则$P(AB)=P(A)P(B)$。
- 应用概率加法公式:$P(A \cup B) = P(A) + P(B) - P(AB)$,将已知条件代入公式,解方程求出$P(B)$。
破题关键点:
- 正确写出独立事件的联合概率表达式。
- 代入已知数值后,正确整理方程并求解。
根据题意,事件A与B独立,因此$P(AB) = P(A)P(B)$。
根据概率加法公式:
$P(A \cup B) = P(A) + P(B) - P(AB)$
将已知条件代入:
$0.7 = 0.4 + P(B) - 0.4 \cdot P(B)$
整理方程:
$0.7 = 0.4 + 0.6P(B)$
移项得:
$0.6P(B) = 0.3 \quad \Rightarrow \quad P(B) = \frac{0.3}{0.6} = 0.5$