题目
设(x)=dfrac (1)(1-{e)^dfrac (x{x-1)}}求f(x)的间断点并判断类型。
设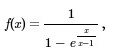 求f(x)的间断点并判断类型。
求f(x)的间断点并判断类型。
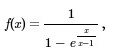 求f(x)的间断点并判断类型。
求f(x)的间断点并判断类型。题目解答
答案
可能的间断点x=0,x=1.
而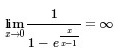 ,
,
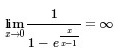 ,
,∴x=0是函数的第二类无穷型间断点。
又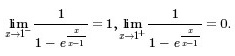
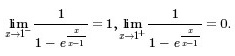
∴x=1是函数的第一类跳跃间断点。
解析
考查要点:本题主要考查函数间断点的求解及类型判断,涉及分母为零、指数函数的极限分析。
解题核心思路:
- 确定无定义点:分母为零或分母中的分母为零的情况。
- 分析极限存在性:分别计算左右极限,判断是否存在及是否相等。
- 分类间断点类型:根据极限是否存在及是否相等,确定为第一类或第二类间断点。
破题关键点:
- 分母为零的点:解方程 $1 - e^{\frac{x}{x-1}} = 0$,得 $x=0$。
- 分母中的分母为零的点:$x=1$。
- 极限分析:特别注意 $x \to 1$ 时,指数 $\frac{x}{x-1}$ 的趋向方向对极限的影响。
步骤1:确定无定义点
- 分母为零:
$1 - e^{\frac{x}{x-1}} = 0 \Rightarrow e^{\frac{x}{x-1}} = 1 \Rightarrow \frac{x}{x-1} = 0 \Rightarrow x = 0$。 - 分母中的分母为零:
$x - 1 = 0 \Rightarrow x = 1$。
可能的间断点:$x=0$ 和 $x=1$。
步骤2:分析 $x=0$ 处的极限
- 当 $x \to 0$ 时,$\frac{x}{x-1} \to 0$,但趋近方向不同:
- $x \to 0^+$:$\frac{x}{x-1} \to 0^-$,$e^{\frac{x}{x-1}} \to 1^-$,分母 $1 - e^{\frac{x}{x-1}} \to 0^+$,故 $f(x) \to +\infty$。
- $x \to 0^-$:$\frac{x}{x-1} \to 0^+$,$e^{\frac{x}{x-1}} \to 1^+$,分母 $1 - e^{\frac{x}{x-1}} \to 0^-$,故 $f(x) \to -\infty$。
- 结论:$\lim_{x \to 0} f(x)$ 不存在,为第二类无穷型间断点。
步骤3:分析 $x=1$ 处的极限
- 当 $x \to 1^-$:
- $\frac{x}{x-1} \to -\infty$,$e^{\frac{x}{x-1}} \to 0$,分母 $1 - 0 = 1$,故 $\lim_{x \to 1^-} f(x) = 1$。
- 当 $x \to 1^+$:
- $\frac{x}{x-1} \to +\infty$,$e^{\frac{x}{x-1}} \to +\infty$,分母 $1 - (+\infty) \to -\infty$,故 $\lim_{x \to 1^+} f(x) = 0$。
- 结论:左右极限存在但不相等,为第一类跳跃间断点。