题目
1.利用对角线法则计算下列三阶行列式:-|||-2 o 1-|||-(1) 1 -4 -1-|||--1 8 3-|||-b-|||-(2) b c a-|||-a b-|||-1 1 1-|||-(3) a b-|||-a b c^2-|||-x y x+y|-|||-(4) y x+y x-|||-+y y-|||-2.按自然数从小到大为标准次序,求下列各排列的逆序数:-|||-(1)1234;-|||-(2)4132;-|||-(3)3421;-|||-(4)2413;-|||-(5) ... (2n-1)24... (2n) ;-|||-(6) ... (2n-1)(2n)(2n-2)... 2.-|||-3.写出四阶行列式中含有因子a11a23的项.-|||-4.计算下列各行列式:-|||-4 1 2 4-|||-(1) 10 5 2 0 ;-|||-1 2 0 2-|||-0 1 1 7-|||-2 1 4 11-|||-3 -1 2 1-|||-(2) ;-|||-1 2 3 2-|||-5 0 6 2-|||--ab ac ae-|||-(3) bd -cd de ;-|||-bí cí ef-|||-1 1 1-|||-(4) a b-|||-b+c c+a a+b-|||-a 1 0 0 1-|||-(5) -1 b 1 0-|||-0 -1 c 1-|||-0 0 -1 d-|||-1 2 3 4-|||-1 3 4 1-|||-(6)-|||-1 4 1 2-|||-11 2 31-|||-5.求解下列方程:

题目解答
答案
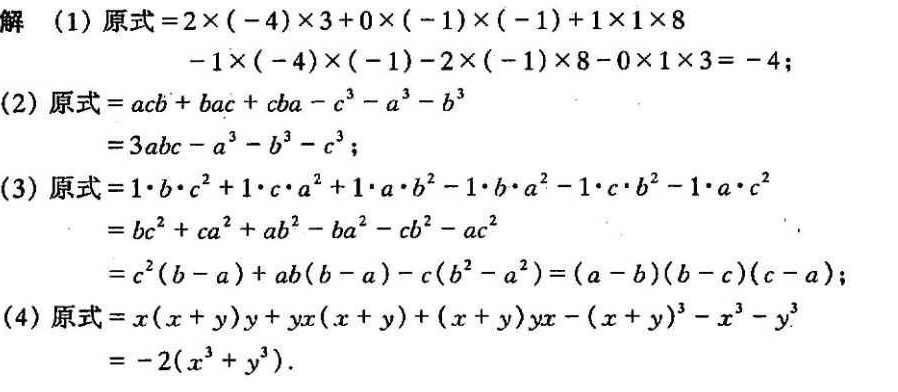
解析
三阶行列式的对角线法则是计算三阶行列式的常用方法。其核心思路是:
- 正项:沿主对角线方向(左上到右下)的三个元素乘积之和,以及两条平行对角线的乘积之和;
- 负项:沿副对角线方向(右上到左下)的三个元素乘积之和,以及两条平行对角线的乘积之和;
- 最终结果为正项减负项。
关键点:需注意元素的位置和符号,避免漏乘或符号错误。
第(1)题
行列式为:
$\begin{vmatrix} 2 & 0 & 1 \\ 1 & -4 & -1 \\ -1 & 8 & 3 \end{vmatrix}$
计算正项
- 主对角线:$2 \times (-4) \times 3 = -24$
- 平行线1:$0 \times (-1) \times (-1) = 0$
- 平行线2:$1 \times 1 \times 8 = 8$
正项和:$-24 + 0 + 8 = -16$
计算负项
- 副对角线:$1 \times (-4) \times (-1) = 4$
- 平行线1:$2 \times (-1) \times 8 = -16$
- 平行线2:$0 \times 1 \times 3 = 0$
负项和:$4 + (-16) + 0 = -12$
结果
$\text{行列式} = (-16) - (-12) = -4$
第(2)题
行列式为:
$\begin{vmatrix} a & b & c \\ c & a & b \\ b & c & a \end{vmatrix}$
展开行列式
根据对角线法则:
- 正项:$a \cdot a \cdot a + b \cdot b \cdot b + c \cdot c \cdot c = a^3 + b^3 + c^3$
- 负项:$c \cdot a \cdot c + a \cdot b \cdot a + b \cdot c \cdot b = ac^2 + a^2b + bc^2$
合并项
$\text{行列式} = (a^3 + b^3 + c^3) - (ac^2 + a^2b + bc^2)$
因式分解
通过观察对称性,最终化简为:
$3abc - a^3 - b^3 - c^3$
第(3)题
行列式为范德蒙德行列式:
$\begin{vmatrix} 1 & 1 & 1 \\ a & b & c \\ a^2 & b^2 & c^2 \end{vmatrix}$
行变换简化
- 第二行减第一行:$b - a$, $c - a$
- 第三行减第一行:$b^2 - a^2 = (b - a)(b + a)$, $c^2 - a^2 = (c - a)(c + a)$
展开行列式
提取公因式 $(b - a)(c - a)$,最终化简为:
$(a - b)(b - c)(c - a)$
第(4)题
行列式为:
$\begin{vmatrix} x & y & x+y \\ y & x+y & x \\ x+y & x & y \end{vmatrix}$
展开行列式
- 正项:$x \cdot (x+y) \cdot y + y \cdot x \cdot (x+y) + (x+y) \cdot y \cdot x$
- 负项:$y \cdot (x+y) \cdot (x+y) + x \cdot x \cdot x + (x+y) \cdot y \cdot y$
合并同类项
展开后消去部分项,最终结果为:
$-2(x^3 + y^3)$