题目
判定函数(z)=dfrac ({x)^2}(2)+xyi在何处可导在何处解析
判定函数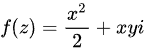 在何处可导在何处解析
在何处可导在何处解析
题目解答
答案
解:已知函数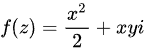 ,
,
令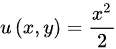 ,
,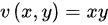 ,
,
则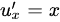 ,
,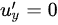 ,
,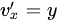 ,
,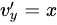 ,
,
由柯西黎曼方程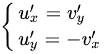 得:
得: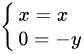 ,
,
所以函数在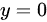 处可导,在复平面上处处不解析.
处可导,在复平面上处处不解析.
解析
考查要点:本题主要考查复变函数的可导性和解析性的判定,核心是应用柯西-黎曼方程。
解题思路:
- 分解函数:将复变函数分解为实部$u(x,y)$和虚部$v(x,y)$。
- 计算偏导数:分别求出$u$和$v$的四个一阶偏导数。
- 代入柯西-黎曼方程:联立方程$\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}$和$\frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}$,求解满足条件的$(x,y)$。
- 判断解析性:若函数在某区域内的每一点都满足柯西-黎曼方程且偏导数连续,则该区域解析;否则不解析。
破题关键:通过柯西-黎曼方程确定可导点,再根据解析的局部性质判断解析区域。
分解函数与计算偏导数
设$f(z) = u(x,y) + iv(x,y)$,其中:
$u(x,y) = \frac{x^2}{2}, \quad v(x,y) = xy$
计算偏导数:
$\frac{\partial u}{\partial x} = x, \quad \frac{\partial u}{\partial y} = 0 \\
\frac{\partial v}{\partial x} = y, \quad \frac{\partial v}{\partial y} = x$
代入柯西-黎曼方程
柯西-黎曼方程为:
$\begin{cases}\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y} \\\frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}\end{cases}$
代入偏导数:
- 第一式:$x = x$,恒成立。
- 第二式:$0 = -y$,解得$y = 0$。
结论:当且仅当$y = 0$时,柯西-黎曼方程成立,即函数在直线$y=0$上可导。
判断解析性
解析要求函数在某邻域内处处可导。由于$y=0$仅是一条直线,不存在包含该点的邻域,因此函数在复平面上处处不解析。