题目
做有理化dfrac (sqrt {x+2)-sqrt (3)}(x-1)
做有理化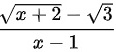
题目解答
答案
解答:
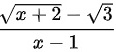
=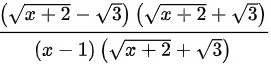
=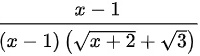
=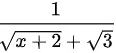
解析
步骤 1:确定有理化因子
为了有理化分母,我们需要找到一个因子,使得分母中的根号被消除。在这个问题中,分母是$x-1$,而分子是$\sqrt{x+2}-\sqrt{3}$。为了消除根号,我们可以使用共轭因子$\sqrt{x+2}+\sqrt{3}$。
步骤 2:乘以共轭因子
将分子和分母同时乘以共轭因子$\sqrt{x+2}+\sqrt{3}$,这样可以消除分子中的根号,同时分母中的$x-1$也会被保留。
步骤 3:简化表达式
分子中的根号将被消除,而分母中的$x-1$将与共轭因子相乘,从而得到一个不含根号的表达式。
为了有理化分母,我们需要找到一个因子,使得分母中的根号被消除。在这个问题中,分母是$x-1$,而分子是$\sqrt{x+2}-\sqrt{3}$。为了消除根号,我们可以使用共轭因子$\sqrt{x+2}+\sqrt{3}$。
步骤 2:乘以共轭因子
将分子和分母同时乘以共轭因子$\sqrt{x+2}+\sqrt{3}$,这样可以消除分子中的根号,同时分母中的$x-1$也会被保留。
步骤 3:简化表达式
分子中的根号将被消除,而分母中的$x-1$将与共轭因子相乘,从而得到一个不含根号的表达式。