题目
例22 设f(x)在[0,1]上连续,证明:-|||-lim _(harrow {0)^+}(int )_(0)^1dfrac (h)({h)^2+(x)^2}f(x)dx=dfrac (pi )(2)f(0).
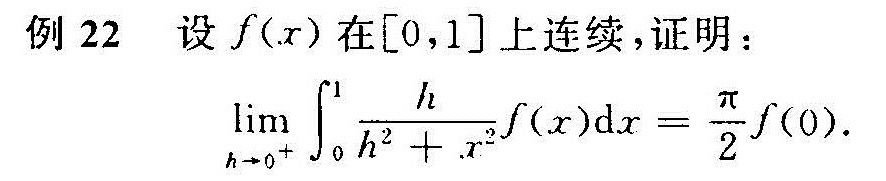
题目解答
答案

解析
步骤 1:定义积分
首先,我们定义积分 ${\int }_{0}^{1}\dfrac {h}{{h}^{2}+{x}^{2}}f(x)dx$,其中 $h$ 是一个趋于零的变量,$f(x)$ 是在 $[0,1]$ 上连续的函数。
步骤 2:拆分积分
将积分拆分为两部分,${I}_{1}={\int }_{0}^{h}\dfrac {h}{{h}^{2}+{x}^{2}}f(x)dx$ 和 ${I}_{2}={\int }_{h}^{1}\dfrac {h}{{h}^{2}+{x}^{2}}f(x)dx$。
步骤 3:应用积分中值定理
对于 ${I}_{1}$,应用积分中值定理,存在 $\xi \in (0,h)$,使得 ${I}_{1}=f(\xi ){\int }_{0}^{h}\dfrac {h}{{h}^{2}+{x}^{2}}dx=f(\xi )\arctan \dfrac {h}{h}=\dfrac {\pi }{2}f(\xi )$。
步骤 4:分析 ${I}_{2}$
对于 ${I}_{2}$,由于 $f(x)$ 在 $[0,1]$ 上连续,存在 $M$ 使得 $|f(x)|\leq M$,因此 ${I}_{2}\leq M{\int }_{h}^{1}\dfrac {h}{{h}^{2}+{x}^{2}}dx\leq M{\int }_{h}^{1}\dfrac {h}{{x}^{2}}dx=Mh\left(\dfrac {1}{h}-1\right)\rightarrow 0$ 当 $h\rightarrow 0$。
步骤 5:求极限
结合步骤 3 和步骤 4,我们得到 ${\int }_{0}^{1}\dfrac {h}{{h}^{2}+{x}^{2}}f(x)dx={I}_{1}+{I}_{2}\rightarrow \dfrac {\pi }{2}f(0)$ 当 $h\rightarrow 0$。
首先,我们定义积分 ${\int }_{0}^{1}\dfrac {h}{{h}^{2}+{x}^{2}}f(x)dx$,其中 $h$ 是一个趋于零的变量,$f(x)$ 是在 $[0,1]$ 上连续的函数。
步骤 2:拆分积分
将积分拆分为两部分,${I}_{1}={\int }_{0}^{h}\dfrac {h}{{h}^{2}+{x}^{2}}f(x)dx$ 和 ${I}_{2}={\int }_{h}^{1}\dfrac {h}{{h}^{2}+{x}^{2}}f(x)dx$。
步骤 3:应用积分中值定理
对于 ${I}_{1}$,应用积分中值定理,存在 $\xi \in (0,h)$,使得 ${I}_{1}=f(\xi ){\int }_{0}^{h}\dfrac {h}{{h}^{2}+{x}^{2}}dx=f(\xi )\arctan \dfrac {h}{h}=\dfrac {\pi }{2}f(\xi )$。
步骤 4:分析 ${I}_{2}$
对于 ${I}_{2}$,由于 $f(x)$ 在 $[0,1]$ 上连续,存在 $M$ 使得 $|f(x)|\leq M$,因此 ${I}_{2}\leq M{\int }_{h}^{1}\dfrac {h}{{h}^{2}+{x}^{2}}dx\leq M{\int }_{h}^{1}\dfrac {h}{{x}^{2}}dx=Mh\left(\dfrac {1}{h}-1\right)\rightarrow 0$ 当 $h\rightarrow 0$。
步骤 5:求极限
结合步骤 3 和步骤 4,我们得到 ${\int }_{0}^{1}\dfrac {h}{{h}^{2}+{x}^{2}}f(x)dx={I}_{1}+{I}_{2}\rightarrow \dfrac {\pi }{2}f(0)$ 当 $h\rightarrow 0$。