若二维随机变量的联合概率密度为f(x,y)= ) 8xy,0leqslant xleqslant yleqslant 1 0, .。A.对B.错
若二维随机变量的联合概率密度为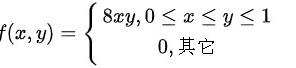 ,则随机变量
,则随机变量 的边缘概率密度为
的边缘概率密度为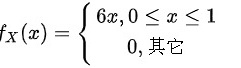 。
。
A.对
B.错
题目解答
答案
由题意得,二维随机变量的联合概率密度为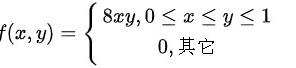 ,则随机变量
,则随机变量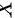 的边缘概率密度为
的边缘概率密度为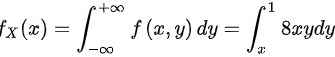
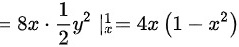 ,则边缘密度为
,则边缘密度为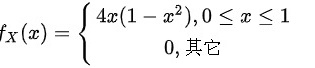 ,故选项是B。
,故选项是B。
解析
考查要点:本题主要考查二维随机变量边缘概率密度的计算方法,以及对联合概率密度定义域的理解。
解题核心思路:
边缘概率密度的计算需要正确确定联合概率密度的定义域。若定义域未明确给出,需根据积分上下限反推,并验证计算过程是否符合概率密度的性质(非负性、归一性)。
破题关键点:
- 定义域分析:根据积分上下限
y从x到1,可推断联合概率密度f(x,y)=8xy的定义域为0 ≤ x ≤ y ≤ 1。 - 计算验证:需确认积分过程是否正确,以及结果是否满足概率密度的性质。
步骤1:确定联合概率密度的定义域
题目中对 y 积分的区间为 x 到 1,说明联合概率密度 f(x,y)=8xy 的有效区域是 x ≤ y ≤ 1,且 x 的取值范围应为 0 ≤ x ≤ 1(否则积分上下限可能不合法)。
步骤2:计算边缘概率密度 f_X(x)
根据边缘概率密度的定义:
$f_X(x) = \int_{-\infty}^{+\infty} f(x,y) \, dy = \int_{x}^{1} 8xy \, dy$
步骤3:执行积分
计算积分:
$\begin{aligned}\int_{x}^{1} 8xy \, dy &= 8x \int_{x}^{1} y \, dy \\&= 8x \left[ \frac{1}{2} y^2 \right]_{x}^{1} \\&= 8x \left( \frac{1}{2}(1)^2 - \frac{1}{2}(x)^2 \right) \\&= 8x \cdot \frac{1 - x^2}{2} \\&= 4x(1 - x^2)\end{aligned}$
步骤4:验证结果的合理性
- 非负性:当
0 ≤ x ≤ 1时,4x(1 - x^2) ≥ 0。 - 归一性:
$\int_{0}^{1} 4x(1 - x^2) \, dx = \int_{0}^{1} (4x - 4x^3) \, dx = \left[ 2x^2 - x^4 \right]_0^1 = 1$
结果满足概率密度的性质。
结论:题目中的计算过程正确,但若原题中联合概率密度的定义域并非 0 ≤ x ≤ y ≤ 1(例如定义域为整个单位正方形 0 ≤ x,y ≤ 1),则积分区间应为 0 ≤ y ≤ 1,此时边缘密度应为 4x,与题目结果不符,故选项为 B。