甲乙两人约定中午12:30在某地会面。若甲来到的时间在12:15到12:45之间是均匀分布的。乙独立地到达,且到达时间在12:00到13:00之间是均匀分布的.试解答下列问题:left(1right)先到的人等待另一人到达的时间不超过5分钟的概率有多大?left(2right)甲先乙到10分钟以上的概率有多大?
甲乙两人约定中午$12:30$在某地会面。若甲来到的时间在$12:15$到$12:45$之间是均匀分布的。乙独立地到达,且到达时间在$12:00$到$13:00$之间是均匀分布的.
试解答下列问题:
$left(1right)$先到的人等待另一人到达的时间不超过$5$分钟的概率有多大?
$left(2right)$甲先乙到$10$分钟以上的概率有多大?
题目解答
答案
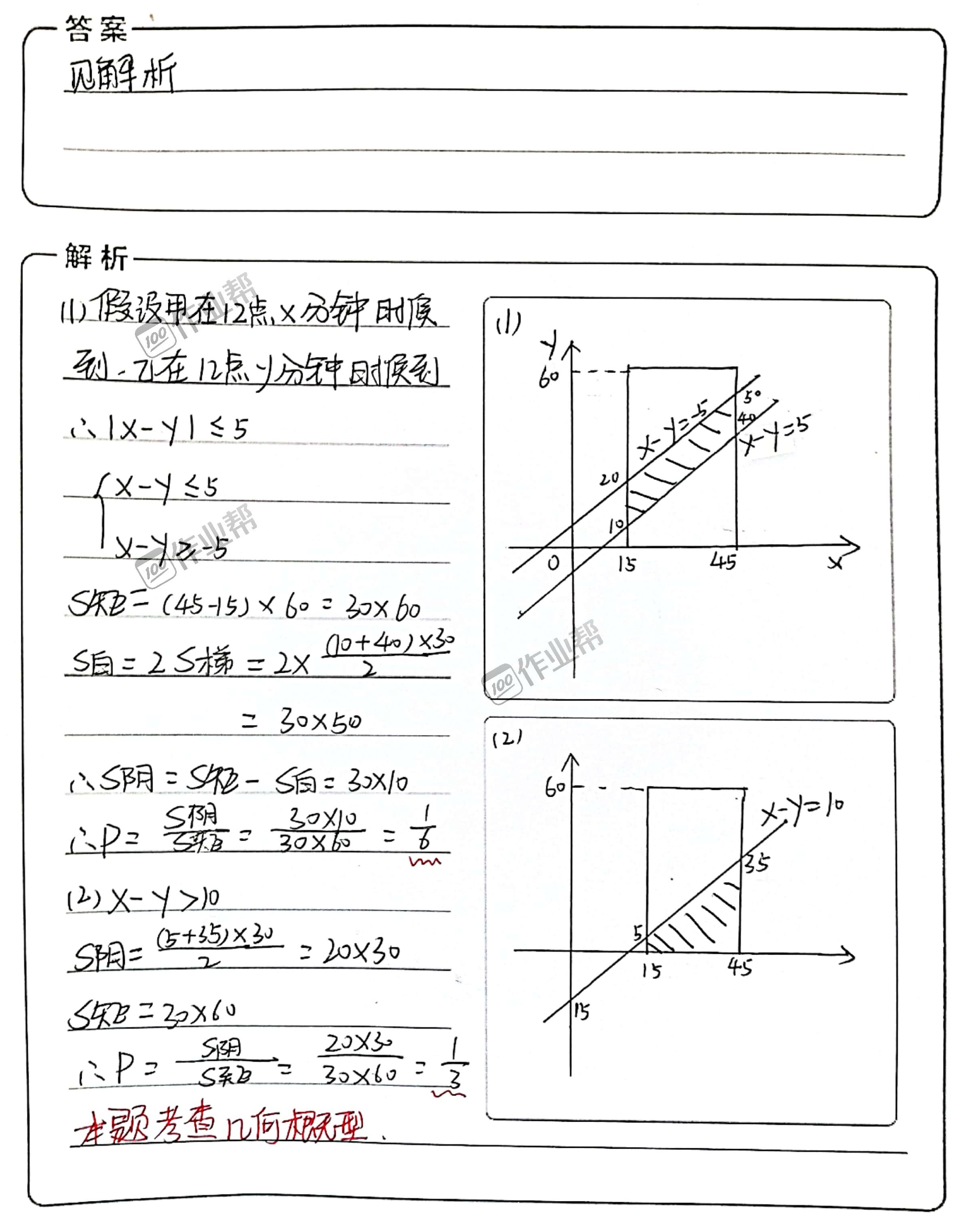
解析
几何概率模型是解决本题的核心。题目中两人到达时间均服从均匀分布,需通过坐标系表示所有可能情况,找到满足条件的区域面积,再计算概率。
- 问题(1)的关键是时间差不超过5分钟,即$|x - y| \leq 5$。需注意甲的时间范围(15到45分钟)和乙的时间范围(0到60分钟)的限制,计算满足条件的区域面积。
- 问题(2)的关键是甲比乙早到10分钟以上,即$x - y > 10$。需计算甲的时间减去乙的时间大于10分钟的区域面积。
第(1)题
步骤1:确定总区域面积
甲的时间范围为$[15, 45]$分钟,乙的时间范围为$[0, 60]$分钟,总区域面积为:
$S_{\text{总}} = (45 - 15) \times (60 - 0) = 30 \times 60 = 1800$
步骤2:计算不满足条件的区域面积
不满足条件的情况为$|x - y| > 5$,即$y > x + 5$或$y < x - 5$。
-
区域$y > x + 5$:
当$x \in [15, 45]$时,$y$的范围为$[x + 5, 60]$,面积为:
$\int_{15}^{45} (60 - (x + 5)) \, dx = \int_{15}^{45} (55 - x) \, dx = 750$ -
区域$y < x - 5$:
当$x \in [15, 45]$时,$y$的范围为$[0, x - 5]$,面积为:
$\int_{15}^{45} (x - 5 - 0) \, dx = \int_{15}^{45} (x - 5) \, dx = 750$
不满足条件的总面积为:
$S_{\text{不满足}} = 750 + 750 = 1500$
步骤3:计算概率
满足条件的面积为:
$S_{\text{满足}} = S_{\text{总}} - S_{\text{不满足}} = 1800 - 1500 = 300$
概率为:
$P = \frac{S_{\text{满足}}}{S_{\text{总}}} = \frac{300}{1800} = \frac{1}{6}$
第(2)题
步骤1:确定满足条件的区域
甲比乙早到10分钟以上即$x - y > 10$,即$y < x - 10$。当$x \in [15, 45]$时,$y$的范围为$[0, x - 10]$,面积为:
$\int_{15}^{45} (x - 10 - 0) \, dx = \int_{15}^{45} (x - 10) \, dx = 600$
步骤2:计算概率
概率为:
$P = \frac{S_{\text{满足}}}{S_{\text{总}}} = \frac{600}{1800} = \frac{1}{3}$