已知函数 z=f(x,y) 连续且满足 lim _(xarrow 1)dfrac (f(x,y)-x+2y+2)(sqrt {{(x-1))^2+(y)^2}}=0 则-|||-lim _(tarrow 0)dfrac (f(1+t,0)-f(1,2t))(t)= __

题目解答
答案
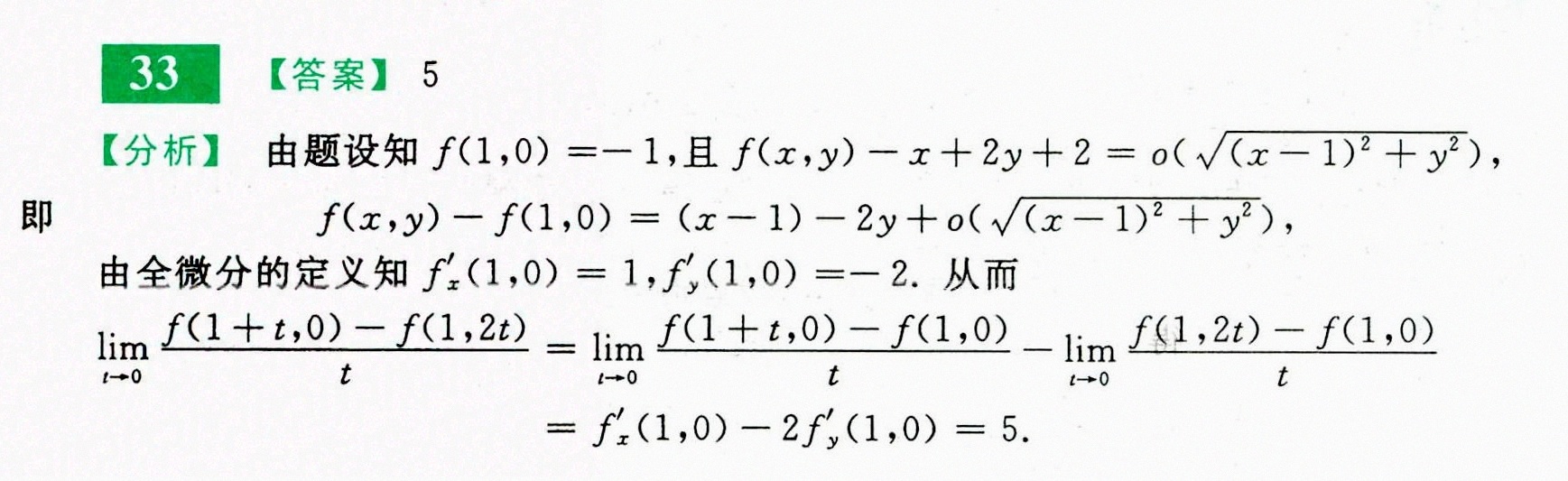
解析
考查要点:本题主要考查多元函数的极限、连续性与偏导数的综合应用,特别是利用全微分的概念求解函数的变化率。
解题核心思路:
- 分析给定极限条件:通过题目中的极限条件,确定函数$f(x,y)$在点$(1,0)$处的函数值及展开式,进而推导偏导数。
- 应用全微分近似:将$f(1+t,0)$和$f(1,2t)$在$(1,0)$处展开,利用偏导数表示函数增量。
- 计算极限:通过展开式求差并取极限,得到最终结果。
破题关键点:
- 确定$f(1,0)$的值:由极限条件可得$f(1,0) = -1$。
- 推导偏导数:通过函数展开式,结合全微分定义,求出$f_x'(1,0)$和$f_y'(1,0)$的值。
步骤1:分析给定极限条件
题目给出:
$\lim _{x\rightarrow 0}\dfrac {f(x,y)-x+2y+2}{\sqrt {{(x-1)}^{2}+{y}^{2}}}=0$
关键推导:
- 当$x \rightarrow 0$时,分母$\sqrt{(x-1)^2 + y^2}$趋近于$\sqrt{1 + y^2}$,但题目实际应理解为$(x,y) \rightarrow (1,0)$(可能存在笔误),此时分母趋近于$0$。
- 分子必须比分母更高阶趋近于$0$,故可表示为:
$f(x,y) - x + 2y + 2 = a(x,y) \cdot \sqrt{(x-1)^2 + y^2}$
其中$a(x,y) \rightarrow 0$当$(x,y) \rightarrow (1,0)$。
结论:$f(1,0) = -1$,且函数展开式为:
$f(x,y) = (x-1) - 2y - 2 + a(x,y) \cdot \sqrt{(x-1)^2 + y^2}$
步骤2:求偏导数
-
对$x$求偏导:
$f_x'(x,y) = 1 + a(x,y) \cdot \frac{x-1}{\sqrt{(x-1)^2 + y^2}}$
当$(x,y) \rightarrow (1,0)$时,第二项中$a(x,y) \rightarrow 0$,故:
$f_x'(1,0) = 1$ -
对$y$求偏导:
$f_y'(x,y) = -2 + a(x,y) \cdot \frac{y}{\sqrt{(x-1)^2 + y^2}}$
当$(x,y) \rightarrow (1,0)$时,第二项中$a(x,y) \rightarrow 0$,故:
$f_y'(1,0) = -2$
步骤3:计算目标极限
将$f(1+t,0)$和$f(1,2t)$展开:
$\begin{aligned}f(1+t,0) &\approx f(1,0) + f_x'(1,0) \cdot t \\f(1,2t) &\approx f(1,0) + f_y'(1,0) \cdot 2t\end{aligned}$
取差并除以$t$:
$\frac{f(1+t,0) - f(1,2t)}{t} \approx \frac{[f(1,0) + f_x'(1,0) \cdot t] - [f(1,0) + f_y'(1,0) \cdot 2t]}{t} = f_x'(1,0) - 2f_y'(1,0)$
代入偏导数值:
$f_x'(1,0) - 2f_y'(1,0) = 1 - 2 \cdot (-2) = 5$