题目
2.设随机变量X的密度为-|||-f(x)= ) cx,0leqslant xleqslant 1 0, ;-|||-(4)X的分布函数F (x).

题目解答
答案
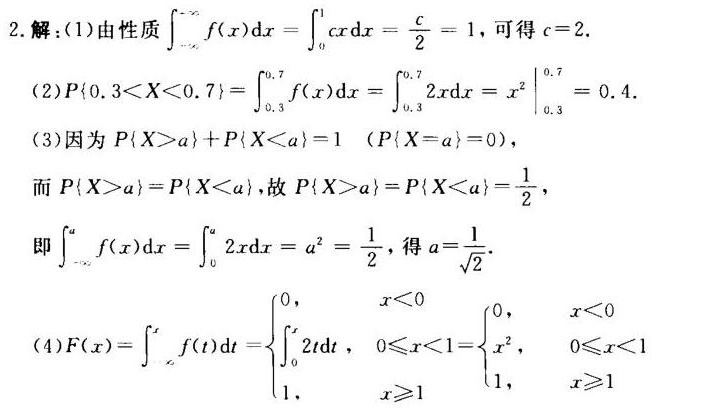
解析
考查要点:本题主要考查概率密度函数的性质、概率计算、对称点求解以及分布函数的构建。
解题核心思路:
- 确定常数c:利用概率密度函数的归一性(积分等于1)求解。
- 计算概率区间:直接对密度函数在区间内积分。
- 求对称点a:通过概率相等条件建立方程,解方程求a。
- 构建分布函数:分段积分密度函数,注意不同区间的积分结果。
破题关键点:
- 归一性:密度函数积分总和为1。
- 分段积分:计算概率时注意积分上下限是否在定义域内。
- 对称点性质:概率相等时对应积分值为1/2。
第(1)题:求常数c
利用归一性
概率密度函数满足:
$\int_{-\infty}^{+\infty} f(x) \, dx = 1$
由于$f(x)=cx$仅在$[0,1]$区间非零,积分简化为:
$\int_{0}^{1} c x \, dx = 1$
计算得:
$\frac{c}{2} = 1 \quad \Rightarrow \quad c = 2$
第(2)题:求$P\{0.3 < X < 0.7\}$
积分计算
概率为密度函数在区间$[0.3, 0.7]$的积分:
$P\{0.3 < X < 0.7\} = \int_{0.3}^{0.7} 2x \, dx = \left[ x^2 \right]_{0.3}^{0.7} = 0.7^2 - 0.3^2 = 0.49 - 0.09 = 0.4$
第(3)题:求常数a
概率相等条件
由$P\{X > a\} = P\{X < a\}$,得:
$P\{X < a\} = \frac{1}{2}$
积分密度函数:
$\int_{0}^{a} 2x \, dx = a^2 = \frac{1}{2} \quad \Rightarrow \quad a = \frac{1}{\sqrt{2}}$
第(4)题:求分布函数$F(x)$
分段积分
- 当$x < 0$时:无密度贡献,$F(x) = 0$。
- 当$0 \leq x < 1$时:
$F(x) = \int_{0}^{x} 2t \, dt = x^2$ - 当$x \geq 1$时:积分覆盖整个定义域,$F(x) = 1$。
综上:
$F(x) =
\begin{cases} 0, & x < 0 \\x^2, & 0 \leq x < 1 \\1, & x \geq 1 \end{cases}$