题目
函数f(x,y)= dfrac (xy)({x)^2+(y)^2},(x)^2+(y)^2neq 0-|||-0, ^2+(y)^2=0在点(0,0)处()。 A.连续,偏导数存在 B.连续,偏导数不存在 C.不连续,偏导数存在 D.不连续,偏导数不存在
函数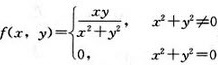 在点(0,0)处()。 A.连续,偏导数存在 B.连续,偏导数不存在 C.不连续,偏导数存在 D.不连续,偏导数不存在
在点(0,0)处()。 A.连续,偏导数存在 B.连续,偏导数不存在 C.不连续,偏导数存在 D.不连续,偏导数不存在
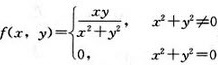 在点(0,0)处()。 A.连续,偏导数存在 B.连续,偏导数不存在 C.不连续,偏导数存在 D.不连续,偏导数不存在
在点(0,0)处()。 A.连续,偏导数存在 B.连续,偏导数不存在 C.不连续,偏导数存在 D.不连续,偏导数不存在题目解答
答案
C
解析
考查要点:本题主要考查二元函数在某点的连续性和偏导数存在性的判断。
解题核心思路:
- 连续性:通过不同路径趋近于原点,判断函数值的极限是否等于函数值(即$f(0,0)=0$)。若存在路径极限不同,则函数在该点不连续。
- 偏导数存在性:直接利用偏导数定义计算$f_x(0,0)$和$f_y(0,0)$,判断极限是否存在。
破题关键点:
- 连续性:沿直线$y=kx$趋近原点时,极限值与$k$相关,说明极限不唯一,函数不连续。
- 偏导数:沿坐标轴方向趋近时,函数值为0,导致偏导数存在且为0。
连续性分析
- 沿x轴趋近:令$y=0$,则$f(x,0)=\dfrac{x \cdot 0}{x^2+0}=0$,极限为$0$。
- 沿y轴趋近:令$x=0$,则$f(0,y)=\dfrac{0 \cdot y}{0+y^2}=0$,极限为$0$。
- 沿直线$y=kx$趋近:代入得:
$f(x,kx)=\dfrac{x \cdot kx}{x^2+(kx)^2}=\dfrac{kx^2}{x^2(1+k^2)}=\dfrac{k}{1+k^2}$
当$x \to 0$时,极限为$\dfrac{k}{1+k^2}$,与$k$相关。例如:- $k=0$时,极限为$0$;
- $k=1$时,极限为$\dfrac{1}{2}$。
结论:沿不同路径极限不同,故$f(x,y)$在$(0,0)$处不连续。
偏导数存在性分析
- 计算$f_x(0,0)$:
$f_x(0,0)=\lim_{h \to 0} \dfrac{f(h,0)-f(0,0)}{h} = \lim_{h \to 0} \dfrac{0-0}{h} = 0$ - 计算$f_y(0,0)$:
$f_y(0,0)=\lim_{k \to 0} \dfrac{f(0,k)-f(0,0)}{k} = \lim_{k \to 0} \dfrac{0-0}{k} = 0$
结论:偏导数存在且均为$0$。