1.计算:(3x+y+2)(3x-y-2).2.已知(3x+y+2)(3x-y-2).求(a+b-c)²。3.设x>0,且(3x+y+2)(3x-y-2).求(3x+y+2)(3x-y-2).的值。4.已知实数x满足(3x+y+2)(3x-y-2).求(3x+y+2)(3x-y-2).的值。
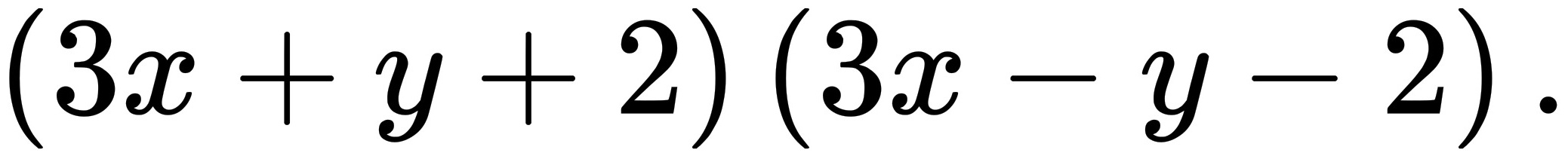
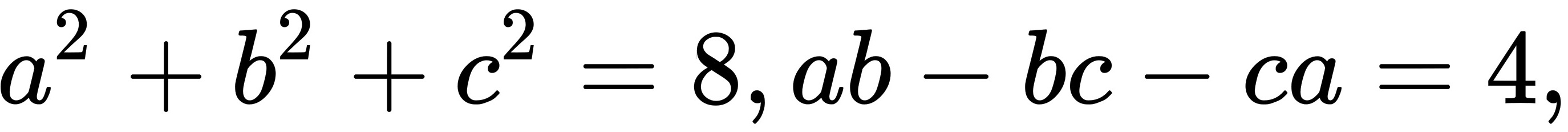 求(a+b-c)²。
求(a+b-c)²。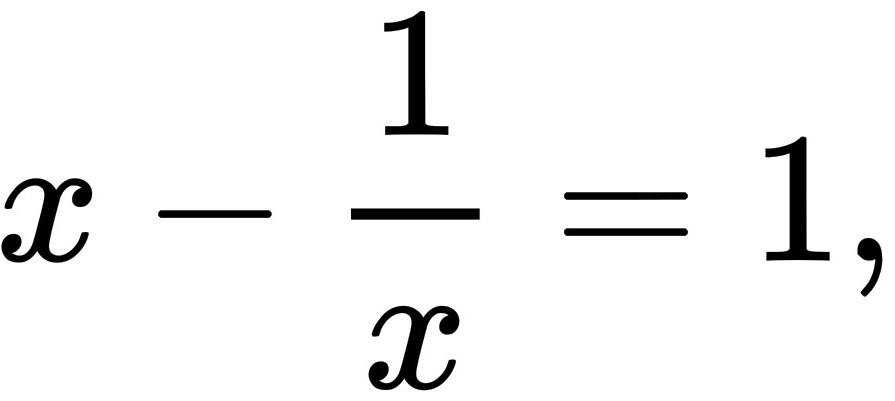 求
求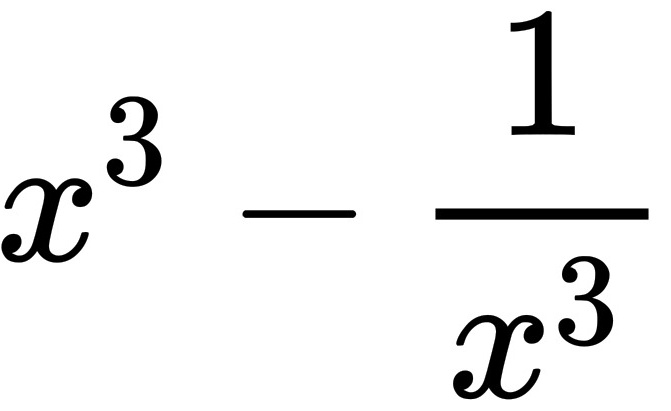 的值。
的值。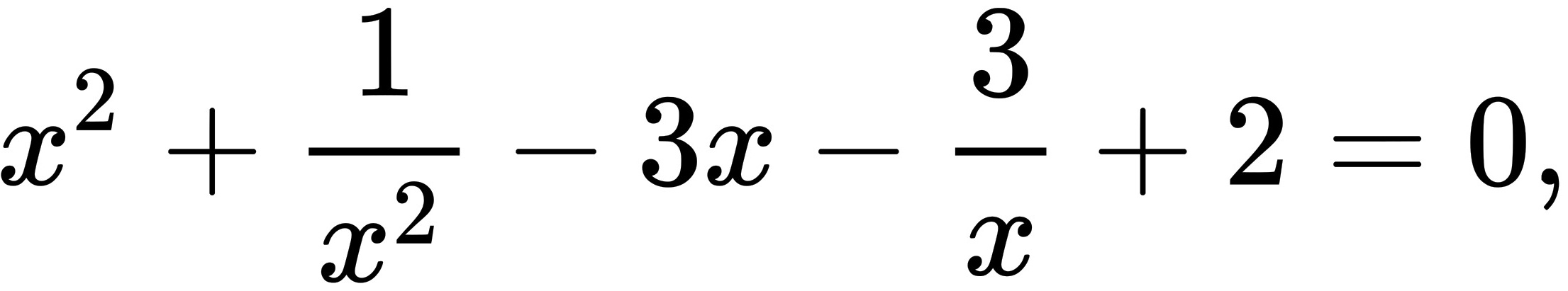 求
求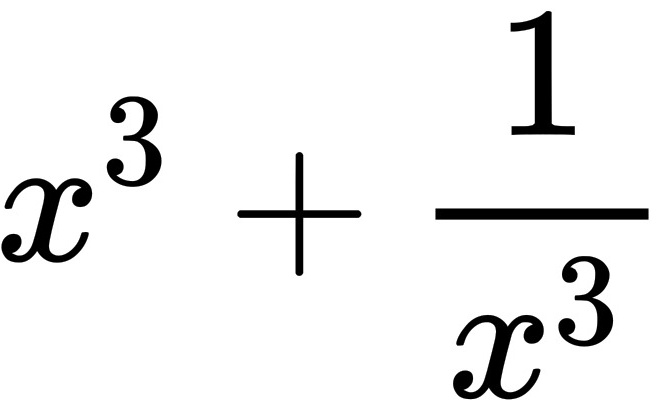 的值。
的值。题目解答
答案
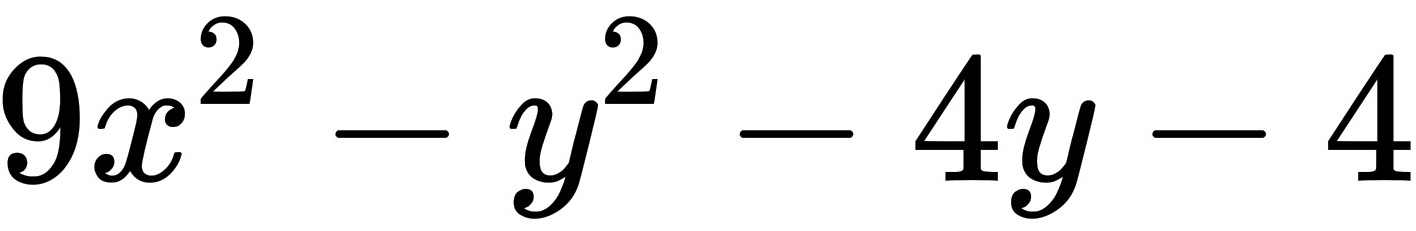
解析
- 多项式乘法:利用平方差公式,将式子转化为两部分的平方差,简化计算。
- 代数恒等式:展开平方后,结合已知条件整体代入。
- 分式与根式的转化:通过平方关系,将高次方程转化为低次表达式。
- 变量代换法:通过设中间变量简化方程,结合立方公式求解。
1. 计算 $(3x + y + 2)(3x - y - 2)$
观察结构,分组处理
将式子看作 $[3x + (y + 2)][3x - (y + 2)]$,符合平方差公式 $(a + b)(a - b) = a^2 - b^2$。
应用公式展开
$\begin{aligned}(3x)^2 - (y + 2)^2 &= 9x^2 - (y^2 + 4y + 4) \\&= 9x^2 - y^2 - 4y - 4.\end{aligned}$
2. 已知 $a^2 + b^2 + c^2 = 8$,$ab - bc - ca = 4$,求 $(a + b - c)^2$
展开平方表达式
$(a + b - c)^2 = a^2 + b^2 + c^2 + 2ab - 2bc - 2ca.$
代入已知条件
$\begin{aligned}a^2 + b^2 + c^2 &= 8, \\2(ab - bc - ca) &= 2 \times 4 = 8.\end{aligned}$
合并结果
$8 + 8 = 16.$
3. 设 $x > 0$,且 $x^2 + \dfrac{1}{x^2} = 14$,求 $x + \dfrac{1}{x}$ 的值
平方关系转化
$\left( x + \dfrac{1}{x} \right)^2 = x^2 + 2 + \dfrac{1}{x^2} = 14 + 2 = 16.$
取正根
$x + \dfrac{1}{x} = \sqrt{16} = 4.$
4. 已知 $x^2 + \dfrac{1}{x^2} - 3x - \dfrac{3}{x} + 2 = 0$,求 $x^3 + \dfrac{1}{x^3}$ 的值
设中间变量
令 $t = x - \dfrac{1}{x}$,则 $t^2 = x^2 - 2 + \dfrac{1}{x^2}$,即 $x^2 + \dfrac{1}{x^2} = t^2 + 2$。
代入方程
$(t^2 + 2) - 3t + 2 = 0 \implies t^2 - 3t + 4 = 0.$
解方程并验证
判别式 $\Delta = 9 - 16 = -7$,无实根,故需重新设变量。
另设变量 $t = x + \dfrac{1}{x}$
原方程变形为:
$(t^2 - 2) - 3t + 2 = 0 \implies t^2 - 3t = 0 \implies t = 0 \text{ 或 } t = 3.$
因 $x > 0$,故 $t = 3$。
求立方值
$x^3 + \dfrac{1}{x^3} = t^3 - 3t = 27 - 9 = 18.$