题目
设甲乙两人轮流地向一目标射击,甲先射击,甲乙每次击中目标的概率分别为0.5和0.6,且每次射击相互不影响,则甲先击中目标的概率为( )A.dfrac (1)(8)A.dfrac (1)(8)A.dfrac (1)(8)A.dfrac (1)(8)
设甲乙两人轮流地向一目标射击,甲先射击,甲乙每次击中目标的概率分别为0.5和0.6,且每次射击相互不影响,则甲先击中目标的概率为( )
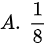
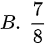
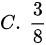
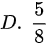
题目解答
答案
设甲先击中目标的概率为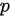
1. 分析情况:
第一次射击甲就击中目标的概率为0.5
若第一次甲未击中目标(概率为1 - 0.5 = 0.5),且乙也未击中目标(概率为1 - 0.6 = 0.4),然后甲第二次射击击中目标,这种情况的概率为0.5×0.4×0.5
若前两轮甲、乙都未击中目标,第三轮甲击中目标,概率为0.5×0.4×0.5×0.4×0.5
2. 建立等式:
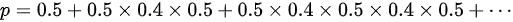
3. 求解概率:
观察上述等式可知,这是一个首项为0.5,公比为0.5×0.4 = 0.2的等比数列求和。
根据等比数列求和公式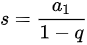 (其中
(其中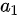 为首项,
为首项,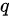 为公比),可得
为公比),可得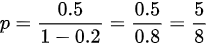
所以甲先击中目标的概率为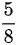 。
。
解析
考查要点:本题主要考查几何分布或无限等比数列求和的应用,涉及独立事件的概率计算。
解题核心思路:
甲在每一轮中可能直接击中目标,或在前一轮双方均未击中后再次获得机会。所有可能情况构成一个首项为甲首次击中概率、公比为双方均未击中的概率的等比数列,求和即可得到甲先击中的总概率。
破题关键点:
- 独立事件:每次射击结果互不影响,概率相乘。
- 无限循环结构:若双方均未击中,问题回到初始状态,形成无限递推。
- 等比数列求和:将所有可能情况转化为等比数列求和,应用公式简化计算。
设甲先击中目标的概率为$p$,分析如下:
第一次射击
甲直接击中的概率为$0.5$,此时甲获胜。
若甲未击中且乙也未击中
- 甲未击中的概率为$1 - 0.5 = 0.5$,乙未击中的概率为$1 - 0.6 = 0.4$。
- 此时双方均未击中,问题回到初始状态,甲再次获得机会,概率为$p$。
- 因此,这种情况的总概率为$0.5 \times 0.4 \times p$。
建立方程
综合以上两种情况,总概率满足:
$p = 0.5 + 0.5 \times 0.4 \times p$
解方程
整理方程:
$p = 0.5 + 0.2p \implies p - 0.2p = 0.5 \implies 0.8p = 0.5 \implies p = \frac{0.5}{0.8} = \frac{5}{8}$