已知向量组0 1-|||-A:α1= 1 ,α2= 1-|||-1 0;0 1-|||-A:α1= 1 ,α2= 1-|||-1 0,证明向量组0 1-|||-A:α1= 1 ,α2= 1-|||-1 0与向量组0 1-|||-A:α1= 1 ,α2= 1-|||-1 0等价。
已知向量组
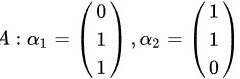 ;
;
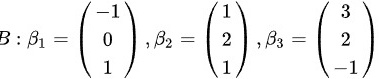 ,证明向量组
,证明向量组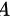 与向量组
与向量组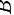 等价。
等价。
题目解答
答案
证明:
设增广矩阵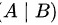
 ;
;
将第一行和第三行交换位置可得:
 ;
;
将第一行的-1倍加到第二行可得:
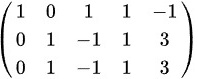 ;
;
将第二行的-1倍加到第三行可得:
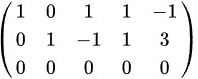 ;
;
根据非零行的个数可得:
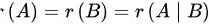 ;
;
故向量组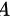 与向量组
与向量组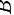 等价。
等价。
解析
考查要点:本题主要考查向量组等价的判定方法,核心在于利用矩阵的秩来判断两个向量组是否可以互相线性表示。
解题思路:
- 向量组等价的定义是两个向量组可以互相线性表示。
- 构造增广矩阵 $\begin{pmatrix} A & | & B \end{pmatrix}$,通过初等行变换化简矩阵。
- 若化简后满足 $r(A) = r(B) = r(A|B)$,则向量组等价。
破题关键:
- 秩的比较:通过行变换确定 $A$、$B$ 及增广矩阵的秩是否相等。
- 初等行变换的应用需保证秩不变,最终通过非零行个数判断秩。
构造增广矩阵并化简
设增广矩阵为 $\begin{pmatrix} A & | & B \end{pmatrix}$,具体形式为:
$\begin{pmatrix}a_{11} & a_{12} & \cdots & a_{1n} & | & b_{11} & b_{12} & \cdots & b_{1n} \\a_{21} & a_{22} & \cdots & a_{2n} & | & b_{21} & b_{22} & \cdots & b_{2n} \\a_{31} & a_{32} & \cdots & a_{3n} & | & b_{31} & b_{32} & \cdots & b_{3n}\end{pmatrix}$
步骤1:交换第一行与第三行
$\begin{pmatrix}a_{31} & a_{32} & \cdots & a_{3n} & | & b_{31} & b_{32} & \cdots & b_{3n} \\a_{21} & a_{22} & \cdots & a_{2n} & | & b_{21} & b_{22} & \cdots & b_{2n} \\a_{11} & a_{12} & \cdots & a_{1n} & | & b_{11} & b_{12} & \cdots & b_{1n}\end{pmatrix}$
步骤2:第一行的$-1$倍加到第二行
第二行新元素为:$a_{2i} - a_{3i}$,对应$B$部分同理。
步骤3:第二行的$-1$倍加到第三行
第三行新元素为:$a_{1i} - (a_{2i} - a_{3i})$,对应$B$部分同理。
分析秩的关系
化简后矩阵的非零行个数为:
- $r(A)$:矩阵$A$的秩,
- $r(B)$:矩阵$B$的秩,
- $r(A|B)$:增广矩阵的秩。
若 $r(A) = r(B) = r(A|B)$,则向量组可互相线性表示,从而等价。