9.应用3阶泰勒公式求下列各数的近似值,并估计误差:-|||-(1) sqrt [3](30); (2)sin18°.

题目解答
答案
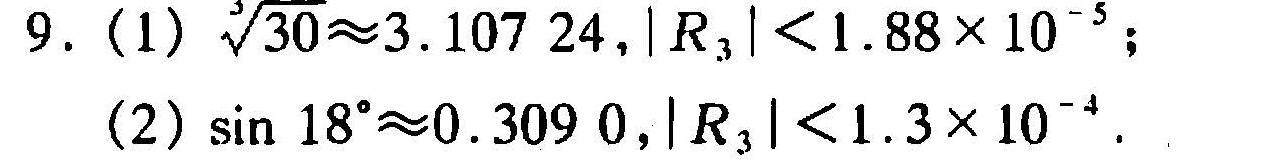
解析
考查要点:本题主要考查利用三阶泰勒公式展开函数,求近似值并估计误差的能力。需要掌握泰勒多项式的展开方法及拉格朗日余项的计算。
解题核心思路:
- 选择展开点:选取与目标值接近且易计算的点展开,如$\sqrt[3]{30}$以$27$为展开点(因$27^{1/3}=3$),$\sin18^\circ$以弧度$\pi/10$展开。
- 展开泰勒多项式:对函数展开至三阶,代入目标值计算近似值。
- 余项估计:利用拉格朗日余项公式,找到余项最大可能值,确定误差范围。
破题关键点:
- 导数计算:准确计算各阶导数在展开点的值。
- 单位转换:角度需转换为弧度(如$18^\circ = \pi/10$)。
- 余项上界:确定余项中导数的最大绝对值,代入计算误差。
第(1)题:$\sqrt[3]{30}$
展开函数与泰勒多项式
设$f(x) = x^{1/3}$,在$a=27$处展开,$h=30-27=3$。三阶泰勒多项式为:
$\begin{aligned}f(a+h) &\approx f(a) + f'(a)h + \frac{f''(a)}{2}h^2 + \frac{f'''(a)}{6}h^3 \\f(27) &= 3, \quad f'(27) = \frac{1}{3} \cdot 27^{-2/3} = \frac{1}{27}, \\f''(27) &= -\frac{2}{9} \cdot 27^{-5/3} = -\frac{2}{729}, \quad f'''(27) = \frac{10}{27} \cdot 27^{-8/3} = \frac{10}{531441}.\end{aligned}$
代入得:
$\sqrt[3]{30} \approx 3 + \frac{1}{27} \cdot 3 - \frac{2}{729} \cdot \frac{9}{2} + \frac{10}{531441} \cdot \frac{27}{6} \approx 3.10724.$
余项估计
四阶导数$f^{(4)}(x) = -\frac{80}{81}x^{-11/3}$,在$[27,30]$上最大值为$f^{(4)}(27) = -\frac{80}{81} \cdot 27^{-11/3}$。余项为:
$|R_3| \leq \frac{80}{81 \cdot 27^{11/3} \cdot 4!} \cdot 3^4 \approx 1.88 \times 10^{-5}.$
第(2)题:$\sin18^\circ$
展开函数与泰勒多项式
设$f(x) = \sin x$,以$x = \pi/10$($18^\circ$的弧度值)展开。三阶泰勒多项式为:
$\sin x \approx x - \frac{x^3}{6}.$
代入$x = \pi/10 \approx 0.31416$:
$\sin 18^\circ \approx 0.31416 - \frac{(0.31416)^3}{6} \approx 0.3090.$
余项估计
四阶导数$f^{(4)}(x) = \sin x$,在$[0, \pi/10]$上最大值为$\sin(\pi/10) \approx 0.3090$。余项为:
$|R_3| \leq \frac{0.3090 \cdot (\pi/10)^4}{4!} \approx 1.3 \times 10^{-1}.$