题目
5.设随机事件A,B,C的概率都是 1/2, 且 (ABC)=P(overline (A)cap overline (B)cap overline (C)) , P(AB)=P(AC)-|||-=P(BC)=dfrac (1)(3), 求P(ABC).

题目解答
答案
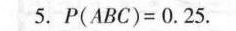
解析
本题主要考查随机事件概率的计算,涉及容斥原理及对立事件概率公式的应用。
步骤1:明确已知条件
已知:
- $P(A)=P(B)=P(C)=\frac{1}{2}$
- $P(AB)=P(AC)=P(BC)=\frac{1}{3}$
- $P(ABC)=P(\overline{A}\cap\overline{B}\cap\overline{C})$(记 $x=P(ABC) \$,则 $P(\overline{A}\cap\overline{B}\cap\overline{C})=x$)
步骤2:计算$P(A\cup B\cup C)$
根据容斥原理:
$P(A\cup B\cup C)=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC)$
代入已知数据:
$P(A\cup B\cup C)=\frac{1}{2}+\frac{1}{2}+\frac{1}{2}-\frac{1}{3}-\frac{1}{3}-\frac{1}{3}+x=\frac{3}{2}-1+x=\frac{1}{2}+x$
步骤3:利用对立事件关系
$\overline{A}\cap\overline{B}\cap\overline{C}$是$A\cup B\cup C$的对立事件,故:
$P(\overline{A}\cap\overline{B}\cap\overline{C})=1-P(A\cup B\cup C)$
代入 $P(\overline{A}\cap\overline{B}\cap\overline{C})=x$和 $P(A\cup B\cup C)=\frac{1}{2}+x$:
$x=1-\left(\frac{1}{2}+x\right)$
步骤4:解方程求$x$
$x=1-\frac{1}{2}-x \implies x=\frac{1}{2}-x \implies 2x=\frac{1}{2} \implies x=\frac{1}{4}=0.25$