题目
下列结论里正确的是( )ydx+xdy=0，其中ydx+xdy=0是ydx+xdy=0平面上的任意光滑正向闭合曲线曲线积分ydx+xdy=0路径无关ydx+xdy=0，其中ydx+xdy=0，取逆时针方向ydx+xdy=0在整个ydx+xdy=0平面内是某一个函数ydx+xdy=0的全微分
下列结论里正确的是( )
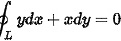，其中
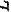是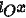
平面上的任意光滑正向闭合曲线- 曲线积分
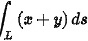路径无关 
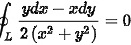，其中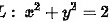
，取逆时针方向
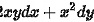在整个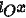平面内是某一个函数
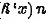的全微分
题目解答
答案
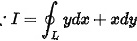
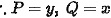
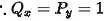
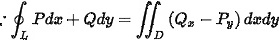
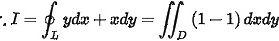
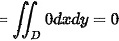
本题选择A选项
解析
步骤 1：分析选项A
对于选项A，给出的积分是$ydx+xdy=0$，其中是Ox平面上的任意光滑正向闭合曲线。根据格林公式，如果$Pdx+Qdy$在闭合曲线上的积分为0，那么$Pdx+Qdy$的全微分形式为$(Q_x-P_y)dxdy$，其中$Q_x$和$P_y$分别是$Q$对$x$的偏导数和$P$对$y$的偏导数。对于$ydx+xdy$，$P=y$，$Q=x$，所以$Q_x=1$，$P_y=1$，因此$Q_x-P_y=0$，所以$ydx+xdy$的积分在任意光滑正向闭合曲线上为0。
步骤 2：分析选项B
对于选项B，给出的积分是${\int }_{I}(x+y)ds$，其中$I$是路径。这个积分表示的是路径$I$上$(x+y)$的线积分。由于没有给出$I$的具体形式，我们不能确定这个积分是否与路径无关。因此，选项B不能确定。
步骤 3：分析选项C
对于选项C，给出的积分是$\dfrac {ydx-xdy}{2({x}^{2}+{y}^{2})}=0$，其中${x}^{2}+{y}^{2}=2$，取逆时针方向。这个积分表示的是在圆${x}^{2}+{y}^{2}=2$上$\dfrac {ydx-xdy}{2({x}^{2}+{y}^{2})}$的线积分。由于${x}^{2}+{y}^{2}=2$是一个圆，所以这个积分可以使用格林公式来计算。根据格林公式，如果$Pdx+Qdy$在闭合曲线上的积分为0，那么$Pdx+Qdy$的全微分形式为$(Q_x-P_y)dxdy$，其中$Q_x$和$P_y$分别是$Q$对$x$的偏导数和$P$对$y$的偏导数。对于$\dfrac {ydx-xdy}{2({x}^{2}+{y}^{2})}$，$P=\dfrac {y}{2({x}^{2}+{y}^{2})}$，$Q=-\dfrac {x}{2({x}^{2}+{y}^{2})}$，所以$Q_x=-\dfrac {1}{2({x}^{2}+{y}^{2})}$，$P_y=\dfrac {1}{2({x}^{2}+{y}^{2})}$，因此$Q_x-P_y=-\dfrac {1}{2({x}^{2}+{y}^{2})}-\dfrac {1}{2({x}^{2}+{y}^{2})}=-\dfrac {1}{{x}^{2}+{y}^{2}}$，所以$\dfrac {ydx-xdy}{2({x}^{2}+{y}^{2})}$的积分在圆${x}^{2}+{y}^{2}=2$上为$-\dfrac {1}{{x}^{2}+{y}^{2}}$的积分，即$-\dfrac {1}{2}$。
步骤 4：分析选项D
对于选项D，给出的积分是$2yydx+{x}^{2}dy$在整个Ox平面内是某一个函数$f(x,y)$的全微分。根据全微分的定义，如果$Pdx+Qdy$是某一个函数$f(x,y)$的全微分，那么$Pdx+Qdy$的全微分形式为$(Q_x-P_y)dxdy$，其中$Q_x$和$P_y$分别是$Q$对$x$的偏导数和$P$对$y$的偏导数。对于$2yydx+{x}^{2}dy$，$P=2yy$，$Q={x}^{2}$，所以$Q_x=2x$，$P_y=2y$，因此$Q_x-P_y=2x-2y$，所以$2yydx+{x}^{2}dy$的积分在整个Ox平面内不是某一个函数$f(x,y)$的全微分。
对于选项A，给出的积分是$ydx+xdy=0$，其中是Ox平面上的任意光滑正向闭合曲线。根据格林公式，如果$Pdx+Qdy$在闭合曲线上的积分为0，那么$Pdx+Qdy$的全微分形式为$(Q_x-P_y)dxdy$，其中$Q_x$和$P_y$分别是$Q$对$x$的偏导数和$P$对$y$的偏导数。对于$ydx+xdy$，$P=y$，$Q=x$，所以$Q_x=1$，$P_y=1$，因此$Q_x-P_y=0$，所以$ydx+xdy$的积分在任意光滑正向闭合曲线上为0。
步骤 2：分析选项B
对于选项B，给出的积分是${\int }_{I}(x+y)ds$，其中$I$是路径。这个积分表示的是路径$I$上$(x+y)$的线积分。由于没有给出$I$的具体形式，我们不能确定这个积分是否与路径无关。因此，选项B不能确定。
步骤 3：分析选项C
对于选项C，给出的积分是$\dfrac {ydx-xdy}{2({x}^{2}+{y}^{2})}=0$，其中${x}^{2}+{y}^{2}=2$，取逆时针方向。这个积分表示的是在圆${x}^{2}+{y}^{2}=2$上$\dfrac {ydx-xdy}{2({x}^{2}+{y}^{2})}$的线积分。由于${x}^{2}+{y}^{2}=2$是一个圆，所以这个积分可以使用格林公式来计算。根据格林公式，如果$Pdx+Qdy$在闭合曲线上的积分为0，那么$Pdx+Qdy$的全微分形式为$(Q_x-P_y)dxdy$，其中$Q_x$和$P_y$分别是$Q$对$x$的偏导数和$P$对$y$的偏导数。对于$\dfrac {ydx-xdy}{2({x}^{2}+{y}^{2})}$，$P=\dfrac {y}{2({x}^{2}+{y}^{2})}$，$Q=-\dfrac {x}{2({x}^{2}+{y}^{2})}$，所以$Q_x=-\dfrac {1}{2({x}^{2}+{y}^{2})}$，$P_y=\dfrac {1}{2({x}^{2}+{y}^{2})}$，因此$Q_x-P_y=-\dfrac {1}{2({x}^{2}+{y}^{2})}-\dfrac {1}{2({x}^{2}+{y}^{2})}=-\dfrac {1}{{x}^{2}+{y}^{2}}$，所以$\dfrac {ydx-xdy}{2({x}^{2}+{y}^{2})}$的积分在圆${x}^{2}+{y}^{2}=2$上为$-\dfrac {1}{{x}^{2}+{y}^{2}}$的积分，即$-\dfrac {1}{2}$。
步骤 4：分析选项D
对于选项D，给出的积分是$2yydx+{x}^{2}dy$在整个Ox平面内是某一个函数$f(x,y)$的全微分。根据全微分的定义，如果$Pdx+Qdy$是某一个函数$f(x,y)$的全微分，那么$Pdx+Qdy$的全微分形式为$(Q_x-P_y)dxdy$，其中$Q_x$和$P_y$分别是$Q$对$x$的偏导数和$P$对$y$的偏导数。对于$2yydx+{x}^{2}dy$，$P=2yy$，$Q={x}^{2}$，所以$Q_x=2x$，$P_y=2y$，因此$Q_x-P_y=2x-2y$，所以$2yydx+{x}^{2}dy$的积分在整个Ox平面内不是某一个函数$f(x,y)$的全微分。