设下面所考虑的函数都是定义在区间-1,1)上的,证明:(1)两个偶函数的和是偶函数,两个奇函数的和是奇函数(2)两个偶函数的乘积是偶函数,两个奇函数的乘积是偶函数,偶函数与奇函数的乘积是奇函数
设下面所考虑的函数都是定义在区间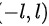 上的,证明:
上的,证明:
(1)两个偶函数的和是偶函数,两个奇函数的和是奇函数
(2)两个偶函数的乘积是偶函数,两个奇函数的乘积是偶函数,偶函数与奇函数的乘积是奇函数
题目解答
答案
(1)设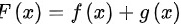
1.如果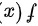 和
和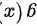 都是偶函数,则
都是偶函数,则
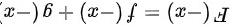
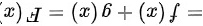
所以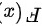 为偶函数,即两个偶函数的和是偶函数
为偶函数,即两个偶函数的和是偶函数
2.如果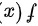 和
和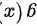 都是奇函数,则
都是奇函数,则
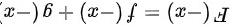
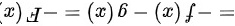
所以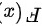 为奇函数,即两个奇函数的和是奇函数
为奇函数,即两个奇函数的和是奇函数
(2)设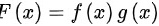
1.如果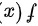 和
和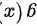 都是偶函数,则
都是偶函数,则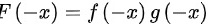
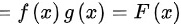
所以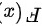 为偶函数,即两个偶函数的乘积是偶函数
为偶函数,即两个偶函数的乘积是偶函数
2.如果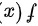 和
和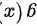 都是奇函数,则
都是奇函数,则
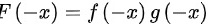
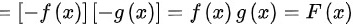
所以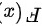 为奇函数,即两个奇函数的乘积是奇函数
为奇函数,即两个奇函数的乘积是奇函数
3.如果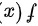 是偶函数,
是偶函数,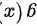 都是奇函数,则
都是奇函数,则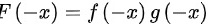
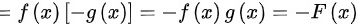
所以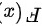 为奇函数,即偶函数与奇函数的乘积是奇函数
为奇函数,即偶函数与奇函数的乘积是奇函数
通过以上分析即可推出正确结论
解析
考查要点:本题主要考查函数奇偶性的定义及其运算性质,需要根据偶函数和奇函数的定义,通过代数运算验证和与乘积的奇偶性。
解题核心思路:
- 偶函数定义:$f(-x) = f(x)$;
- 奇函数定义:$f(-x) = -f(x)$;
- 关键操作:对和或乘积函数进行变量替换$-x$,结合原函数的奇偶性,推导结果的奇偶性。
破题关键点:
- 和的奇偶性:通过逐项代入定义,符号叠加判断整体性质;
- 乘积的奇偶性:通过符号相乘规律,结合偶函数与奇函数的符号特性推导结果。
第(1)题:和的奇偶性
设和函数为$F(x) = f(x) + g(x)$
-
若$f(x)$和$g(x)$均为偶函数:
$F(-x) = f(-x) + g(-x) = f(x) + g(x) = F(x)$
因此$F(x)$是偶函数。 -
若$f(x)$和$g(x)$均为奇函数:
$F(-x) = f(-x) + g(-x) = -f(x) - g(x) = -F(x)$
因此$F(x)$是奇函数。
第(2)题:乘积的奇偶性
设乘积函数为$F(x) = f(x) \cdot g(x)$
-
若$f(x)$和$g(x)$均为偶函数:
$F(-x) = f(-x) \cdot g(-x) = f(x) \cdot g(x) = F(x)$
因此$F(x)$是偶函数。 -
若$f(x)$和$g(x)$均为奇函数:
$F(-x) = f(-x) \cdot g(-x) = (-f(x)) \cdot (-g(x)) = f(x) \cdot g(x) = F(x)$
因此$F(x)$是偶函数。 -
若$f(x)$是偶函数,$g(x)$是奇函数:
$F(-x) = f(-x) \cdot g(-x) = f(x) \cdot (-g(x)) = -f(x) \cdot g(x) = -F(x)$
因此$F(x)$是奇函数。