题目
设某人有3个不同的电子邮件账户,有70%的邮件进入账户1,另有20%的邮件进入账户2,其余10%的邮件进入账户3,根据以往经验,3个账户垃圾邮件的比例分别为1%,2%,5%,求:(1)某天随机收到一封邮件为垃圾邮件的概率;(2)随机打开了一封邮件发现是垃圾邮件,该邮件来自账户2的概率.
设某人有3个不同的电子邮件账户,有70%的邮件进入账户1,另有20%的邮件进入账户2,其余10%的邮件进入账户3,根据以往经验,3个账户垃圾邮件的比例分别为1%,2%,5%,求:
(1)某天随机收到一封邮件为垃圾邮件的概率;
(2)随机打开了一封邮件发现是垃圾邮件,该邮件来自账户2的概率.
题目解答
答案
(1)来自账户1中的垃圾邮件的概率为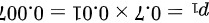 ,
,
来自账户2中的垃圾邮件的概率为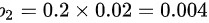 ,
,
来自账户3中的垃圾邮件的概率为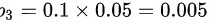 ,
,
则垃圾邮件的全概率为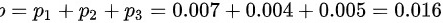 ;(2)随机打开了一封邮件发现是垃圾邮件,则该邮件来自账户2的条件概率为
;(2)随机打开了一封邮件发现是垃圾邮件,则该邮件来自账户2的条件概率为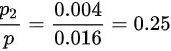 .
.
解析
考查要点:本题主要考查全概率公式和贝叶斯定理的应用,涉及条件概率的理解与计算。
解题核心思路:
- 第(1)问:计算随机收到垃圾邮件的概率,需将各账户垃圾邮件的概率加权求和,权重为各账户的邮件占比。
- 第(2)问:已知邮件是垃圾邮件,求来自账户2的条件概率,需用贝叶斯定理,即用账户2的垃圾邮件概率除以总垃圾邮件概率。
破题关键点:
- 正确拆分事件:将垃圾邮件来源分为三个互斥的账户。
- 准确计算各部分概率:注意百分比转换为小数,并正确应用乘法原理。
第(1)题
计算各账户垃圾邮件的概率
- 账户1:邮件占比$70\%$(即$0.7$),垃圾比例$1\%$(即$0.01$),垃圾概率为:
$P_1 = 0.7 \times 0.01 = 0.007$ - 账户2:邮件占比$20\%$(即$0.2$),垃圾比例$2\%$(即$0.02$),垃圾概率为:
$P_2 = 0.2 \times 0.02 = 0.004$ - 账户3:邮件占比$10\%$(即$0.1$),垃圾比例$5\%$(即$0.05$),垃圾概率为:
$P_3 = 0.1 \times 0.05 = 0.005$
总垃圾邮件概率
将各账户垃圾概率相加:
$P(\text{垃圾}) = P_1 + P_2 + P_3 = 0.007 + 0.004 + 0.005 = 0.016$
第(2)题
应用贝叶斯定理
已知邮件是垃圾邮件,来自账户2的条件概率为:
$P(\text{账户2} \mid \text{垃圾}) = \frac{P(\text{垃圾} \mid \text{账户2}) \cdot P(\text{账户2})}{P(\text{垃圾})} = \frac{0.004}{0.016} = 0.25$