题目
设A是秩为m的 times n 矩阵,且 lt n, 则非齐次线性方程组 AX=b __ ...
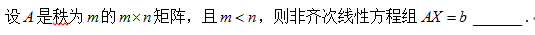
题目解答
答案

解析
步骤 1:理解矩阵的秩
矩阵A的秩为m,意味着矩阵A的行空间和列空间的维度都是m。由于A是一个 $m\times n$ 矩阵,且 $m\lt n$,说明矩阵A的列数大于行数,即矩阵A的列向量组线性相关。
步骤 2:分析非齐次线性方程组的解
非齐次线性方程组AX=b的解的个数取决于系数矩阵A的秩和增广矩阵[A|b]的秩。如果增广矩阵[A|b]的秩等于系数矩阵A的秩,那么方程组有解。由于A的秩为m,且m
步骤 3:确定解的个数
由于A的秩为m,且m
矩阵A的秩为m,意味着矩阵A的行空间和列空间的维度都是m。由于A是一个 $m\times n$ 矩阵,且 $m\lt n$,说明矩阵A的列数大于行数,即矩阵A的列向量组线性相关。
步骤 2:分析非齐次线性方程组的解
非齐次线性方程组AX=b的解的个数取决于系数矩阵A的秩和增广矩阵[A|b]的秩。如果增广矩阵[A|b]的秩等于系数矩阵A的秩,那么方程组有解。由于A的秩为m,且m
步骤 3:确定解的个数
由于A的秩为m,且m