题目
int dfrac (1+2{x)^2}({x)^2(1+(x)^2})dx_____.
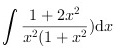
_____.
题目解答
答案
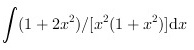
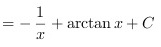
解析
考查要点:本题主要考查分式积分的计算,特别是通过部分分式分解将复杂分式转化为简单分式的和,进而逐项积分的能力。
解题核心思路:
观察到分母为$x^2(1+x^2)$,分子为$1+2x^2$,可通过分子拆分将原分式分解为$\frac{1}{x^2} + \frac{1}{1+x^2}$的和,从而简化积分过程。
破题关键点:
- 分子重组:将分子$1+2x^2$拆分为$(1+x^2)+x^2$,与分母形成可分离的结构。
- 分式分解:通过拆分后的分子,将原分式分解为两个简单分式的和,分别对应基本积分公式。
将被积函数$\frac{1+2x^2}{x^2(1+x^2)}$进行拆分:
-
分子拆分:
$1 + 2x^2 = (1 + x^2) + x^2$ -
分式分解:
$\frac{1+2x^2}{x^2(1+x^2)} = \frac{(1+x^2) + x^2}{x^2(1+x^2)} = \frac{1+x^2}{x^2(1+x^2)} + \frac{x^2}{x^2(1+x^2)} = \frac{1}{x^2} + \frac{1}{1+x^2}$ -
逐项积分:
- $\int \frac{1}{x^2} \, dx = -\frac{1}{x} + C_1$
- $\int \frac{1}{1+x^2} \, dx = \arctan x + C_2$
-
合并结果:
$\int \frac{1+2x^2}{x^2(1+x^2)} \, dx = -\frac{1}{x} + \arctan x + C$