题目
15.设A,B是两事件,且P(A)=0.6,P(B)=0.8,问:(1)在什么条件下P(AB)取到最大值,最大值是多少?(2)在什么条件下P(AB)取得最小值,最小值是多少?
15.设A,B是两事件,且P(A)=0.6,P(B)=0.8,问:
(1)在什么条件下P(AB)取到最大值,最大值是多少?
(2)在什么条件下P(AB)取得最小值,最小值是多少?
题目解答
答案
解:(1)因为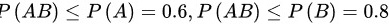
所以当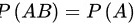 时,
时,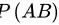 的最大值是0.6
的最大值是0.6
(2)因为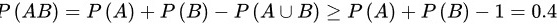
所以有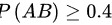 .而当
.而当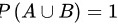 时,有
时,有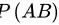 达到最小值0.4.
达到最小值0.4.
解析
考查要点:本题主要考查概率论中事件交的概率极值问题,涉及概率的基本性质和事件间的关系。
解题核心思路:
- 最大值:当两个事件尽可能重叠时,交的概率最大。此时,较小事件完全包含于较大事件中,交的概率等于较小事件的概率。
- 最小值:当两个事件的并集覆盖整个样本空间时,交的概率最小。利用概率加法公式推导最小值。
破题关键点:
- 最大值条件:若事件$A$完全包含于事件$B$,则$P(AB)=P(A)$。
- 最小值公式:$P(AB) \geq P(A) + P(B) - 1$,当$P(A \cup B) = 1$时取到最小值。
第(1)题
分析交的概率上限
根据概率的基本性质,交事件的概率不超过任一事件的概率:
$P(AB) \leq P(A) = 0.6, \quad P(AB) \leq P(B) = 0.8.$
因此,$P(AB)$的最大可能值为$0.6$。
确定最大值条件
当且仅当$A \subseteq B$时,$AB = A$,此时$P(AB) = P(A) = 0.6$。
第(2)题
利用加法公式推导
根据概率加法公式:
$P(A \cup B) = P(A) + P(B) - P(AB).$
由于$P(A \cup B) \leq 1$,整理得:
$P(AB) \geq P(A) + P(B) - 1 = 0.6 + 0.8 - 1 = 0.4.$
确定最小值条件
当$P(A \cup B) = 1$时,$P(AB)$达到最小值$0.4$。