题目
3.设 f(x)= -infty lt xlt 0 sin dfrac {1)(x) 0lt xlt +infty . 求f(x)在x→0时的左极限,并-|||-说明它在x→0时的右极限是否存在?
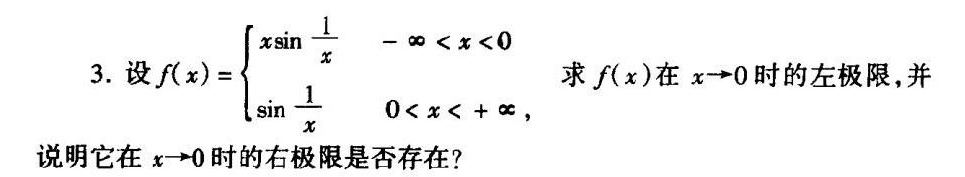
题目解答
答案
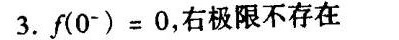
解析
考查要点:本题主要考查分段函数在分段点处的左、右极限是否存在,以及极限的计算方法。
解题核心思路:
- 左极限:当$x \to 0^-$时,函数表达式为$x \sin \frac{1}{x}$,需利用夹逼定理判断极限值。
- 右极限:当$x \to 0^+$时,函数表达式为$\sin \frac{1}{x}$,需分析函数值的震荡性,判断极限是否存在。
破题关键点:
- 左极限的关键在于观察$x$的绝对值随$x \to 0$趋近于0,从而压制度荡的$\sin \frac{1}{x}$项。
- 右极限的关键在于发现$\sin \frac{1}{x}$在$x \to 0^+$时无限次在$[-1,1]$之间震荡,导致极限不存在。
左极限($x \to 0^-$)
当$x \to 0^-$时,$f(x) = x \sin \frac{1}{x}$。
- 分析$\sin \frac{1}{x}$的有界性:
$\forall x \neq 0$,有$|\sin \frac{1}{x}| \leq 1$,因此:
$|x \sin \frac{1}{x}| \leq |x|.$ - 应用夹逼定理:
当$x \to 0^-$时,$|x| \to 0$,故:
$-|x| \leq x \sin \frac{1}{x} \leq |x|.$
根据夹逼定理,$\lim_{x \to 0^-} x \sin \frac{1}{x} = 0$。
右极限($x \to 0^+$)
当$x \to 0^+$时,$f(x) = \sin \frac{1}{x}$。
- 分析震荡性:
当$x \to 0^+$时,$\frac{1}{x} \to +\infty$,$\sin \frac{1}{x}$在$[-1,1]$之间无限次震荡。 - 举例验证极限不存在:
- 取$x_n = \frac{1}{2n\pi}$,则$\sin \frac{1}{x_n} = \sin(2n\pi) = 0$,极限为0。
- 取$y_n = \frac{1}{\frac{\pi}{2} + 2n\pi}$,则$\sin \frac{1}{y_n} = \sin\left(\frac{\pi}{2} + 2n\pi\right) = 1$,极限为1。
由于不同路径的极限值不同,故$\lim_{x \to 0^+} \sin \frac{1}{x}$不存在。