6.设随机变量X的概率密度为-|||-f(x)= ) 3(x)^2,0lt xlt 1 0, .-|||-求:(1)E(X);(2)D (X).
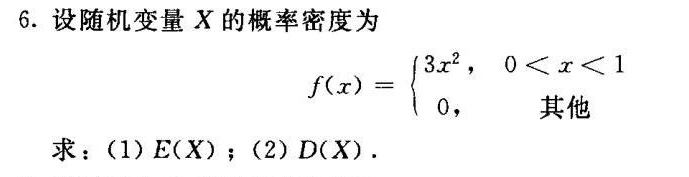
题目解答
答案
解析
考查要点:本题主要考查连续型随机变量的期望与方差的计算,需要熟练掌握概率密度函数的性质以及相关积分运算。
解题核心思路:
- 期望:利用公式 $E(X) = \int_{-\infty}^{+\infty} x f(x) \, dx$,结合概率密度函数的定义域简化积分区间。
- 方差:先计算 $E(X^2)$,再通过公式 $D(X) = E(X^2) - [E(X)]^2$ 得到方差。
破题关键点:
- 积分区间:概率密度函数 $f(x)$ 在 $0 < x < 1$ 时非零,因此积分区间为 $[0, 1]$。
- 积分运算:正确计算幂函数的积分,注意系数和指数的对应关系。
第(1)题:求 $E(X)$
根据期望公式计算
$E(X) = \int_{-\infty}^{+\infty} x f(x) \, dx = \int_{0}^{1} x \cdot 3x^2 \, dx = 3 \int_{0}^{1} x^3 \, dx$
计算积分
$3 \int_{0}^{1} x^3 \, dx = 3 \left[ \frac{x^4}{4} \right]_0^1 = 3 \left( \frac{1}{4} - 0 \right) = \frac{3}{4}$
结论:$E(X) = \dfrac{3}{4}$。
第(2)题:求 $D(X)$
计算 $E(X^2)$
$E(X^2) = \int_{-\infty}^{+\infty} x^2 f(x) \, dx = \int_{0}^{1} x^2 \cdot 3x^2 \, dx = 3 \int_{0}^{1} x^4 \, dx$
计算积分
$3 \int_{0}^{1} x^4 \, dx = 3 \left[ \frac{x^5}{5} \right]_0^1 = 3 \left( \frac{1}{5} - 0 \right) = \frac{3}{5}$
计算方差
$D(X) = E(X^2) - [E(X)]^2 = \frac{3}{5} - \left( \frac{3}{4} \right)^2 = \frac{3}{5} - \frac{9}{16}$
通分运算
$\frac{3}{5} = \frac{48}{80}, \quad \frac{9}{16} = \frac{45}{80}, \quad D(X) = \frac{48}{80} - \frac{45}{80} = \frac{3}{80}$
结论:$D(X) = \dfrac{3}{80}$。