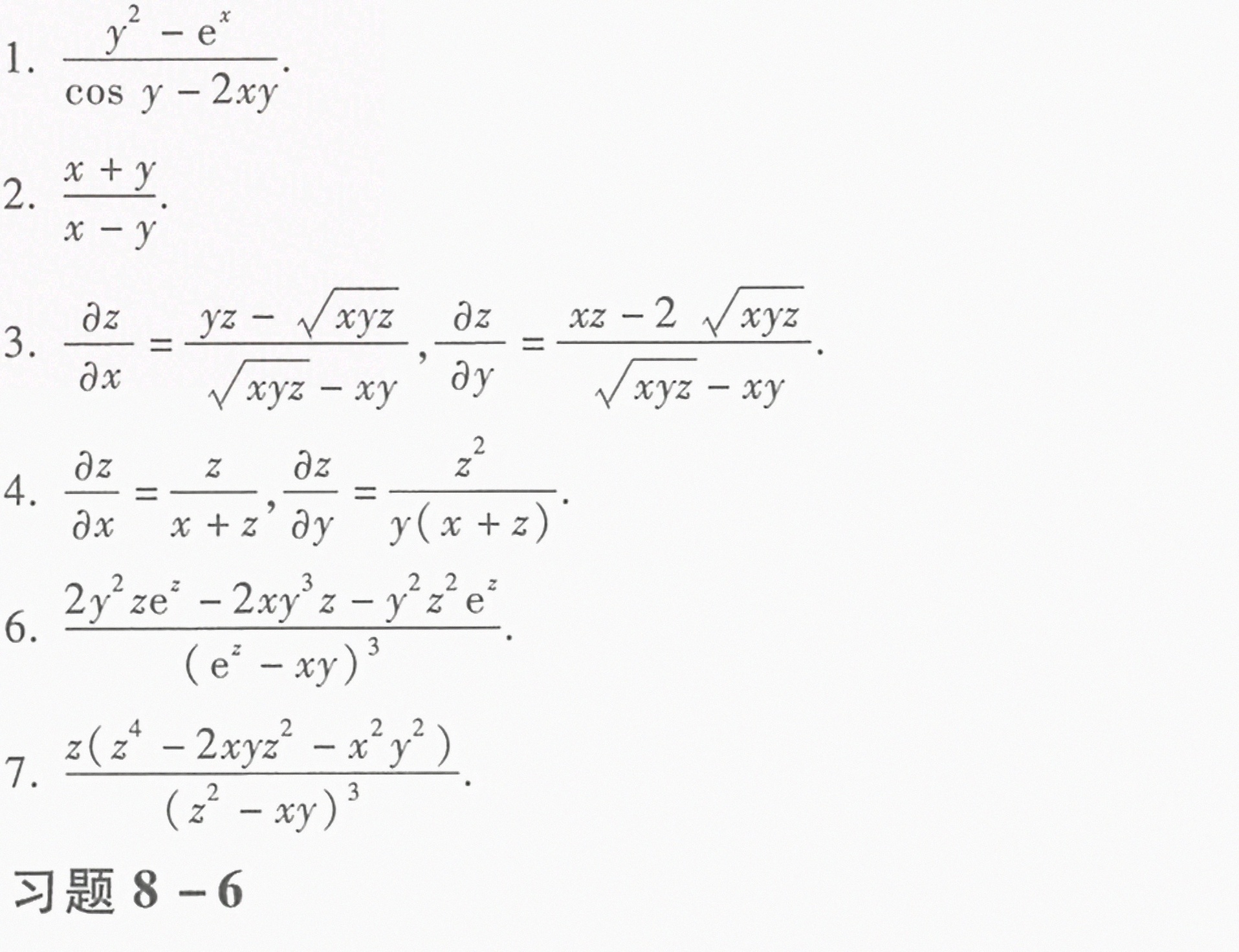题目
1.设 sin y+(e)^x-x(y)^2=0, 求 dfrac (dy)(dx).-|||-2.设 ln sqrt ({x)^2+(y)^2}=arctan dfrac (y)(x), 求 dfrac (dy)(dx).-|||-3.设 +2y+z-2sqrt (xyz)=0, 求 dfrac (partial x)(partial x) 及 dfrac (partial z)(partial y).-|||-4.设 dfrac (x)(z)=ln dfrac (z)(y), 求 dfrac (partial z)(partial x) 及 dfrac (partial z)(partial y).-|||-5.设 sin (x+2y-3z)=x+2y-3z, 证明: dfrac (partial z)(partial x)+dfrac (partial z)(partial y)=1.-|||-6.设 ^z-xyz=0, 求 dfrac ({sigma )^2z}(q{x)^2}-|||-7.设 ^3-3xyz=(a)^3, 求 dfrac ({partial )^2z}(partial xpartial y).
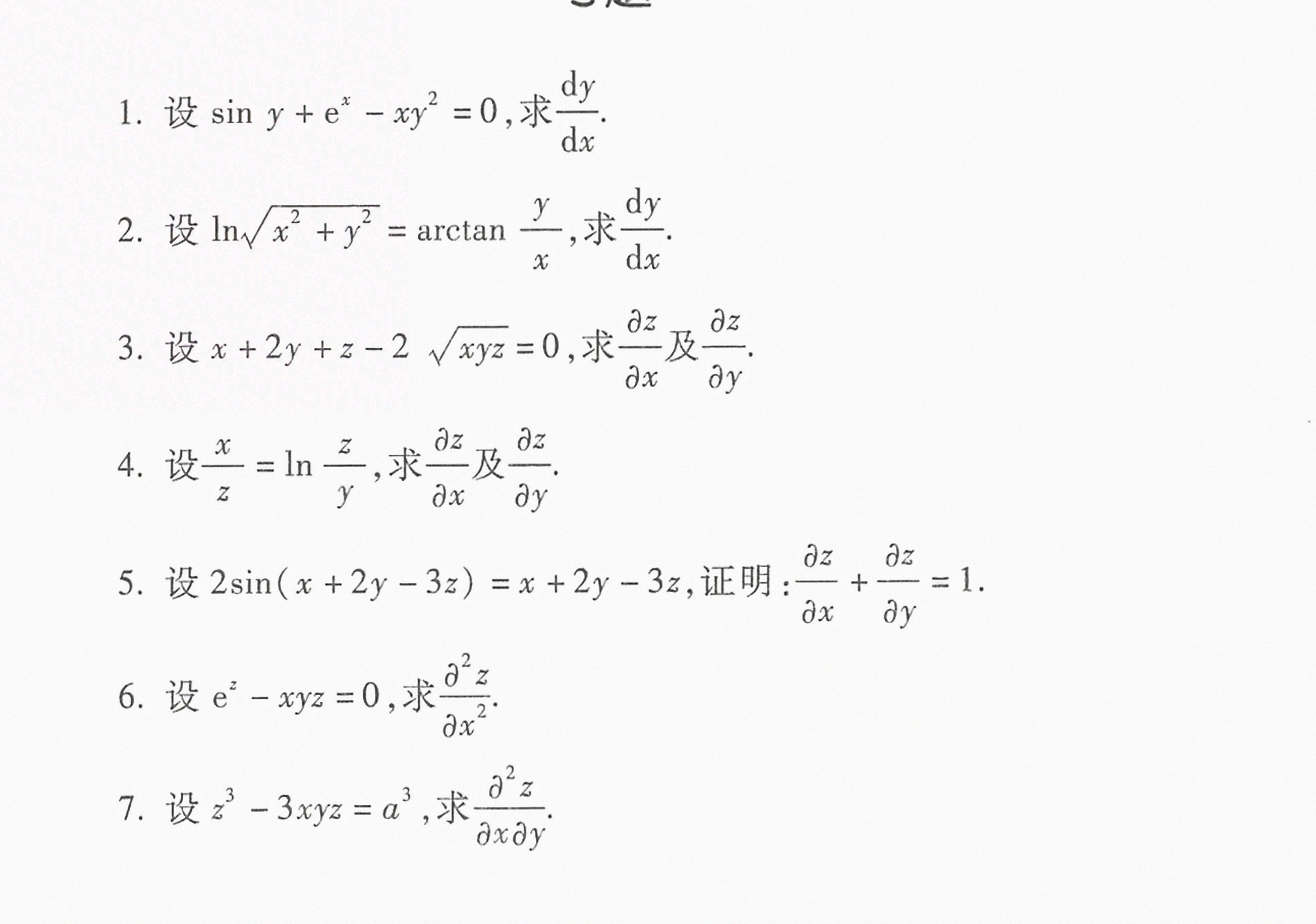
题目解答
答案