题目
f(x)是连续函数, 则 f(x)是f(x)的 ( )A. 一个原函数; B. 一个导函数; C. 全体原函数; D. 全体导函数;
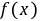 是连续函数, 则
是连续函数, 则 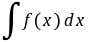 是
是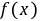 的 ( )
的 ( )
B. 一个导函数;
C. 全体原函数;
D. 全体导函数;
题目解答
答案
C. 全体原函数;
解析
步骤 1:理解原函数的定义
原函数是指一个函数的导数等于另一个函数。如果 $F(x)$ 是 $f(x)$ 的原函数,那么 $F'(x) = f(x)$。
步骤 2:理解不定积分的定义
不定积分 $\int f(x)dx$ 表示所有导数为 $f(x)$ 的函数的集合,即所有 $f(x)$ 的原函数的集合。
步骤 3:分析选项
A. 一个原函数:不定积分表示的是所有原函数,而不仅仅是其中一个。
B. 一个导函数:不定积分表示的是原函数,而不是导函数。
C. 全体原函数:不定积分 $\int f(x)dx$ 表示所有导数为 $f(x)$ 的函数的集合,即所有 $f(x)$ 的原函数的集合。
D. 全体导函数:不定积分表示的是原函数,而不是导函数。
原函数是指一个函数的导数等于另一个函数。如果 $F(x)$ 是 $f(x)$ 的原函数,那么 $F'(x) = f(x)$。
步骤 2:理解不定积分的定义
不定积分 $\int f(x)dx$ 表示所有导数为 $f(x)$ 的函数的集合,即所有 $f(x)$ 的原函数的集合。
步骤 3:分析选项
A. 一个原函数:不定积分表示的是所有原函数,而不仅仅是其中一个。
B. 一个导函数:不定积分表示的是原函数,而不是导函数。
C. 全体原函数:不定积分 $\int f(x)dx$ 表示所有导数为 $f(x)$ 的函数的集合,即所有 $f(x)$ 的原函数的集合。
D. 全体导函数:不定积分表示的是原函数,而不是导函数。