题目
通过点(2,-3,-5)且与平面6x-3y-5z+2=0垂直的直线为( ) 。A、dfrac (x-2)(6)=dfrac (y+3)(-3)=dfrac (z+5)(-5)B、dfrac (x-2)(6)=dfrac (y+3)(-3)=dfrac (z+5)(-5)C、dfrac (x-2)(6)=dfrac (y+3)(-3)=dfrac (z+5)(-5)D、dfrac (x-2)(6)=dfrac (y+3)(-3)=dfrac (z+5)(-5)
通过点(2,-3,-5)且与平面6x-3y-5z+2=0垂直的直线为( ) 。
- A、
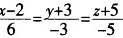
- B、
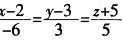
- C、
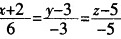
- D、
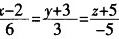
题目解答
答案
A. $\dfrac {x-2}{6}=\dfrac {y+3}{-3}=\dfrac {z+5}{-5}$
解析
步骤 1:确定平面的法向量
平面6x-3y-5z+2=0的法向量为(6, -3, -5)。
步骤 2:确定直线的方向向量
由于直线与平面垂直,所以直线的方向向量与平面的法向量相同,即(6, -3, -5)。
步骤 3:写出直线的参数方程
直线通过点(2,-3,-5),方向向量为(6, -3, -5),所以直线的参数方程为:
x = 2 + 6t
y = -3 - 3t
z = -5 - 5t
步骤 4:将直线的参数方程转换为对称式方程
将直线的参数方程转换为对称式方程,得到:
$\dfrac {x-2}{6}=\dfrac {y+3}{-3}=\dfrac {z+5}{-5}$
平面6x-3y-5z+2=0的法向量为(6, -3, -5)。
步骤 2:确定直线的方向向量
由于直线与平面垂直,所以直线的方向向量与平面的法向量相同,即(6, -3, -5)。
步骤 3:写出直线的参数方程
直线通过点(2,-3,-5),方向向量为(6, -3, -5),所以直线的参数方程为:
x = 2 + 6t
y = -3 - 3t
z = -5 - 5t
步骤 4:将直线的参数方程转换为对称式方程
将直线的参数方程转换为对称式方程,得到:
$\dfrac {x-2}{6}=\dfrac {y+3}{-3}=\dfrac {z+5}{-5}$