题目
求微分方程 dfrac (dy)(dx)=dfrac (y)(x) 的通解.
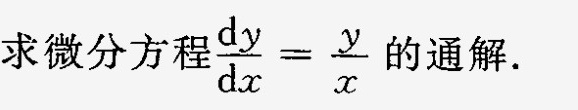
题目解答
答案

解析
本题考察可分离变量的微分方程的求解方法,核心思路是通过分离变量变量、积分并化简得到通解。
步骤1:分离变量
原方程为 $\frac{dy}{dx} = \frac{y}{x}$,当 $y \neq 0$ 时,可将变量 $x$ 和 和 $y$ 分离到等式两侧:
$\frac{dy}{y} = \frac{dx}{x}$
步骤2:积分求解积分
对等式两端积分:
$\int \frac{1}{y}dy = \int \frac{1}{x}dx$
积分结果为:
$\ln|y| = \ln|x| + C_1 \quad (C_1 \text{为任意常数})$
步骤3:化简通解
利用对数性质 $e^{\ln|a|}=|a$,等式两端取指数:
$|y| = e^{C_1}|x|$
令 $(C = \pm e^{C_1}$($C$ 为非零常数),则 $y = Cx$。注意 $y=0$ 也是方程的解,当 $C=0$ 时 $y=0$ 包含在 $y=Cx中,因此通解为 \(y=Cx$($C$ 为任意常数)。
简化运算技巧
为方便运算,可直接写 $\ln y = \ln x + \ln C$(默认 $x,y>0$ 或\ x,y<0)),直接得 $y=Cx$。