题目
某单位的仓库里有来自三个厂家提供的的同一种原材料,它们外形没有区别。甲厂的一级品率为0.95, 乙厂的一级品率为0.98,丙厂的一级品率为0.90。甲、乙、丙三厂的该原材料所占比例为2:2:1。(1)在仓库里随机地取一件该原材料,求它是一级品的概率。(2)在仓库里随机地取一件该原材料,若已知它是一级品,求它是来自甲厂的概率。
某单位的仓库里有来自三个厂家提供的的同一种原材料,它们外形没有区别。甲厂的一级品率为0.95, 乙厂的一级品率为0.98,丙厂的一级品率为0.90。甲、乙、丙三厂的该原材料所占比例为2:2:1。(1)在仓库里随机地取一件该原材料,求它是一级品的概率。(2)在仓库里随机地取一件该原材料,若已知它是一级品,求它是来自甲厂的概率。
题目解答
答案
解: 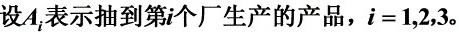
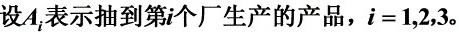
 .
.由全概率公式和贝叶斯公式有
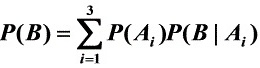
=0.4*0.95+0.4*0.98+0.2*0.9
=0.952.
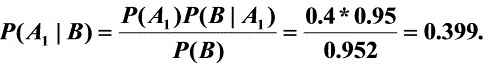
2003-2004学年
解析
考查要点:本题主要考查全概率公式和贝叶斯公式的应用,涉及条件概率的理解与计算。
解题思路:
- 问题(1):要求计算随机取一件原材料是一级品的概率。需将各厂的一级品率与其所占比例(先验概率)相乘后求和,即应用全概率公式。
- 问题(2):已知取到一级品,求来自甲厂的概率。需用贝叶斯公式,计算甲厂贡献的一级品概率占总一级品概率的比例。
关键点:
- 比例转换为概率:甲、乙、丙的比例2:2:1对应概率分别为0.4、0.4、0.2。
- 全概率公式的正确应用:总概率是各分项概率的加权和。
- 贝叶斯公式的分子为甲厂的一级品贡献,分母为问题(1)的结果。
第(1)题
设$A_1, A_2, A_3$分别表示抽到甲、乙、丙厂的产品,$B$表示抽到一级品。根据题意:
- $P(A_1) = 0.4$,$P(A_2) = 0.4$,$P(A_3) = 0.2$
- $P(B|A_1) = 0.95$,$P(B|A_2) = 0.98$,$P(B|A_3) = 0.90$
全概率公式:
$P(B) = \sum_{i=1}^{3} P(A_i)P(B|A_i) = 0.4 \times 0.95 + 0.4 \times 0.98 + 0.2 \times 0.90$
计算过程:
- $0.4 \times 0.95 = 0.38$
- $0.4 \times 0.98 = 0.392$
- $0.2 \times 0.90 = 0.18$
- 总和:$0.38 + 0.392 + 0.18 = 0.952$
第(2)题
贝叶斯公式:
$P(A_1|B) = \frac{P(A_1)P(B|A_1)}{P(B)} = \frac{0.4 \times 0.95}{0.952}$
计算过程:
- 分子:$0.4 \times 0.95 = 0.38$
- 分母:$P(B) = 0.952$(来自第(1)题)
- 结果:$\frac{0.38}{0.952} \approx 0.399$