题目
如图，AB为⊙O的直径，F为弦AC的中点，连接OF并延长交widehat(AC)于点D，过点D作⊙O的切线，交BA的延长线于点E.D C-|||-F-|||-E A 0-|||-B(1)求证：AC∥DE；(2)连接CD，若OA=AE=a，求四边形ACDE的面积.
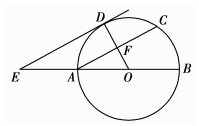
如图，AB为⊙O的直径，F为弦AC的中点，连接OF并延长交$\widehat{AC}$于点D，过点D作⊙O的切线，交BA的延长线于点E.
(1)求证：AC∥DE；
(2)连接CD，若OA=AE=a，求四边形ACDE的面积.
题目解答
答案
(1)证明：∵F为弦AC的中点，
∴OD⊥AC，
∵DE是圆O的切线，
∴OD⊥DE，∴AC∥DE.
(2)求解思路如下：
①在Rt△ODE中，由OA=AE=OD=a可得△ODE，△OFA为含30°的直角三角形；
②由∠ACD=$\frac{1}{2}$∠AOD=30°可得CD∥OE；
③由AC∥DE可得四边形ACDE是平行四边形；
④由△ODE，△OFA为含有30°的直角三角形，可求DE、DF的长，进而求出四边形ACDE的面积.