题目
判断下列命题的真假: (1)点 P到圆心 O的距离大于圆的半径是点 P在 O=外的充要条件; (2)两个三角形的面积相等是这两个三角形全等的充分不必要条件; (3) O=是 O=的必要不充分条件; (4) x或 y为有理数是 xy为有理数的既不充分又不必要条件.
判断下列命题的真假:
(1)点 P到圆心 O的距离大于圆的半径是点 P在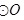 外的充要条件;
外的充要条件;
(2)两个三角形的面积相等是这两个三角形全等的充分不必要条件;
(3)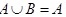 是
是
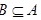 的必要不充分条件;
的必要不充分条件;
(4) x或 y为有理数是 xy为有理数的既不充分又不必要条件.
(1)点 P到圆心 O的距离大于圆的半径是点 P在
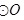 外的充要条件;
外的充要条件;
(2)两个三角形的面积相等是这两个三角形全等的充分不必要条件;
(3)
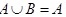 是
是
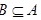 的必要不充分条件;
的必要不充分条件;
(4) x或 y为有理数是 xy为有理数的既不充分又不必要条件.
题目解答
答案
(1)真命题;(2)假命题;(3)假命题;(4)真命题.
解析
考查要点:本题主要考查条件关系的判断,涉及充要条件、充分不必要条件、必要不充分条件、既不充分也不必要的条件的区分。
解题核心思路:
- 明确条件类型定义:充要条件(互为充分必要)、充分不必要(前者是后者的充分条件但非必要)、必要不充分(前者是后者的必要条件但非充分)、既不充分也不必要。
- 逐一分析命题:将每个命题中的两个陈述转化为逻辑关系,判断前者对后者的条件类型。
破题关键点:
- 几何与集合关系:如圆外点与距离的关系、集合的并集与子集关系。
- 反例的构造:通过构造反例判断条件是否成立(如面积相等但三角形不全等,或xy有理但x、y均无理)。
第(1)题
命题:点P到圆心O的距离大于圆的半径是点P在⊙O外的充要条件。
分析:
- 充要条件要求两者互为充分必要条件。
- 圆的定义:点P在圆外当且仅当$|PO| > r$,反之亦然。
- 结论:命题为真。
第(2)题
命题:两个三角形的面积相等是这两个三角形全等的充分不必要条件。
分析:
- 全等三角形面积一定相等,但面积相等的三角形不一定全等(如底3高4与底6高2的三角形)。
- 条件关系:面积相等是全等的必要条件(而非充分条件)。
- 结论:命题为假。
第(3)题
命题:$A \cup B = A$是$B \subseteq A$的必要不充分条件。
分析:
- 集合运算:$A \cup B = A$等价于$B \subseteq A$。
- 条件关系:两者是充要条件关系。
- 结论:命题为假。
第(4)题
命题:x或y为有理数是xy为有理数的既不充分又不必要条件。
分析:
- 充分性:若x或y为有理数,xy未必有理(如$x=1$, $y=\sqrt{2}$,则$xy=\sqrt{2}$无理)。
- 必要性:若xy为有理数,x和y可能均为无理数(如$x=\sqrt{2}$, $y=\sqrt{2}$,则$xy=2$有理)。
- 结论:命题为真。